Die Ableitung
Die Ableitung einer Funktion ist wiederum eine Funktion:
Kennen wir diese, dann können wir damit an jedem Punkt einer Kurve die Steigung berechnen. Von besonderem Interesse sind dabei die Punkte, an denen die Steigung null ist, also die Tangente waagerecht bzw. parallel zur x-Achse verläuft und auch solche Punkte, an denen sich das Ganze wendet:
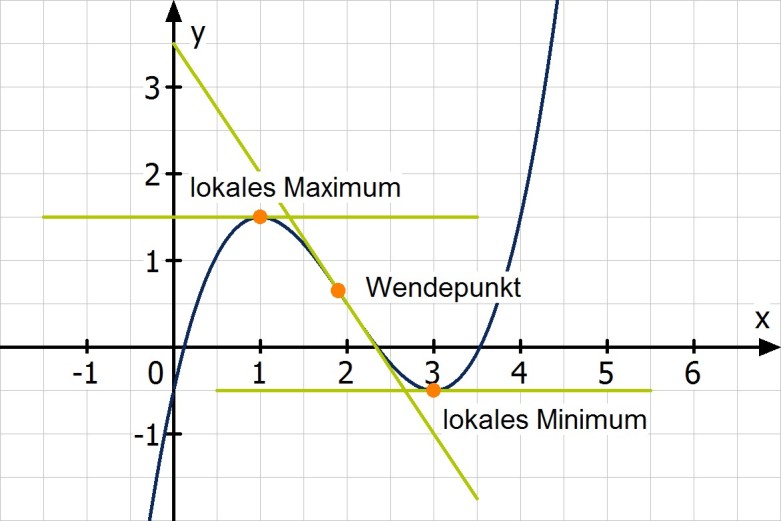
Man denke dabei z.B. an eine Gewinnfunktion. Es macht schon Sinn zu wissen, wie vieler Mengeneinheiten es bedarf um überhaupt Gewinn zu machen und wo dieser am höchsten ist. Der Vorteil der Differenzialrechnung besteht darin, dass wir Extremstellen direkt bestimmen können.
Berechnung der Ableitung an einer bestimmten Stelle , am Beispiel einer quadratischen Funktion, mit der h-Methode (beachte die binomische Formel):
Alternativ kann man auch zuerst den Differenzenquotienten d aufstellen (mit h ≠ 0), dann vereinfachen und erst zum Schluss den Grenzwert für ermitteln:
Berechnung der Ableitungsfunktion, also der Steigung bzw. momentanen Änderungsrate an einer beliebigen Stelle dieser Funktion:
Aus Vereinfachungsgründen steht an Stelle von x0 nur x
Probe:
Für Fortgeschrittene: Herleitung einer allgemeinen Formel für die Ableitung von Potenzfunktionen n-ten Grades (Potenzregel):
T steht für Term
