Gebrochenrationale Funktionen
Gebrochenrationale Funktionen sind Funktionen, die aus einer Zählerfunktion und einer Nennerfunktion bestehen:
Sie weisen gegenüber ganzrationalen Funktionen Besonderheiten auf, denn die Variable – hier x – steht bei echt gebrochenrationalen Funktionen (auch) im Nenner.
Direkt zum Zahlenbeispiel
1. Definitionsbereich
Da man durch Null nicht dividieren kann, ist eine gebrochenrationale Funktion an diesen Stellen nicht definiert:
Setzt man die Nennerfunktion gleich null, erhält man diese Definitionslücken. Da es an diesen Stellen keine Funktionswerte gibt, hat der Graph der Funktion dort auch keine Punkte. Man muss allerdings zwei mögliche Fälle unterscheiden:
a) Polstellen: und an dieser Stelle ist
b) Hebbare Lücke(n): und an dieser Stelle ist auch
(gilt nicht, wenn diese Stelle beim Kürzen als Definitionslücke erhalten bliebe ⇒ dann Polstelle)
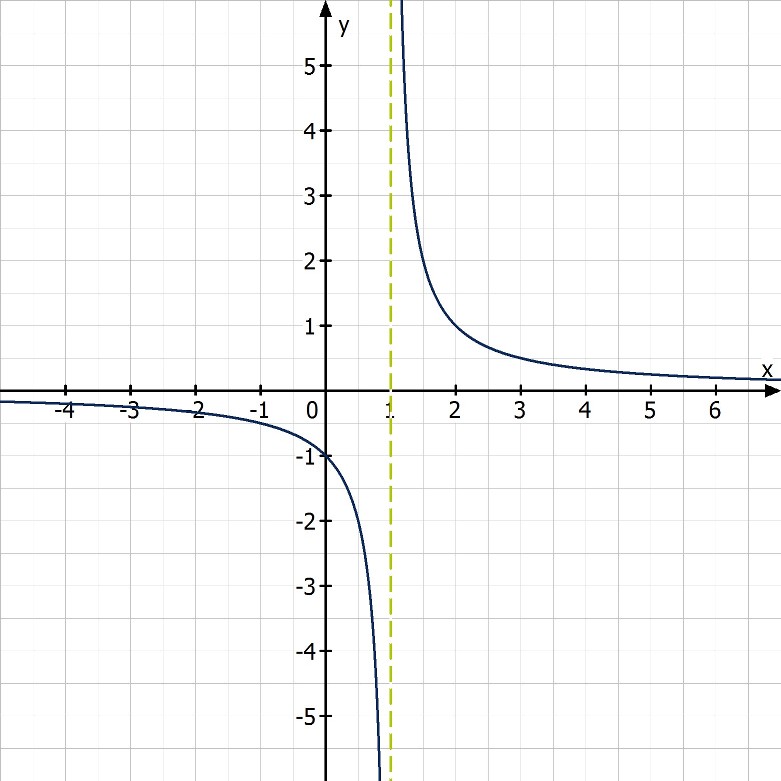
An Polstellen nähert sich der Graph einer gedachten Senkrechten. Er verläuft entlang dieser Linie entweder nach oben oder unten
. Da er sich dieser Geraden nur nähert, sie aber nicht berührt, handelt es sich um eine senkrechte Asymptote mit der Gleichung
2. Schnittpunkte mit der x-Achse (Nullstellen)
Um die Nullstellen einer gebrochenrationalen Funktion zu bestimmen, reicht es aus, die Zählerfunktion gleich null zu setzen:
Die Verfahren zum Lösen solcher Gleichungen sind dieselben, wie beim Auffinden der Nullstellen ganzrationaler Funktionen.
3. Polstellen und hebbare Lücken
An Polstellen untersucht man den Vorzeichenwechsel der Funktionswerte, indem man sich der oder den Asymptote(n) sowohl von links, als auch von rechts nähert. Am einfachsten geht das, indem man für x Zahlen einsetzt, die nahe der Polstelle(n) liegen.
Mit dem Grenzwert (limes) hat man die Möglichkeit, quasi so zu tun, als ob man dieser Stelle ganz nah käme. Man betrachtet dabei, wie sich die Funktionswerte ändern, wenn x verändert wird. Entweder werden die Funktionswerte immer größer (der Graph der Funktion verläuft nach oben), oder sie werden immer kleiner (der Graph der Funktion verläuft nach unten).
Die Polstelle dieser Funktion lautet x = 1. Sie weist einen Vorzeichenwechsel (kurz: VZW) von – nach + auf. Bei einer Wertetabelle würde man den Übergang sofort am Wechsel der Vorzeichen erkennen. Man schreibt:
von links: von rechts:
Es kann aber auch keinen VZW geben.
4. Randverhalten
Bei der Analyse des Randverhaltens möchte man wissen, wie sich die Funktionswerte im Bereich immer größer oder kleiner werdendem x verhalten – also am linken und rechten Rand des Schaubildes. Im Beispiel von oben nähern sie sich der x-Achse. Diese ist in diesem Fall die waagerechte Asymptote mit der Gleichung y = 0. Aber auch das muss nicht immer so sein. Es gibt Merkmale, an denen man sehr leicht ablesen kann, woran sich der Graph anschmiegt:
| Verhältnis | Gleichung der Asymptoten | Aussehen |
| Zählergrad < Nennergrad | y = 0 | x-Achse |
| Zählergrad = Nennergrad | y = b | Parallele zur x-Achse |
| Zahlergrad um eins > Nennergrad | y = mx + b | Schräge Gerade |
Der Grad wird durch die größte Hochzahl bestimmt
In den ersten beiden Fällen ermittelt man die Gleichung der waagerechten Asymptote durch Anwendung der Grenzwertsätze. Im dritten Fall zerlegt man die Funktion durch Polynomdivision in einen ganzrationalen und gebrochenrationalen Anteil. Der ganzrationale Teil bildet die Gleichung der Asymptote.
Zahlenbeispiel
Gegeben ist folgende gebrochenrationale Funktion:
Aufgabe: Vollständige Funktionsuntersuchung mit Definitionsbereich, Achsenschnittpunkten, Polstellen, Verhalten an den Polstellen und an den Rändern, Extrem- und Wendepunkte (wenn vorhanden), Graph.
1. Definitionsbereich und Polstellen
Zur Bestimmung des Definitionsbereichs setzt man die Nennerfunktion gleich null. Wenn man 2 ausklammert, sollte man die dritte binomische Formel erkennen:
Binomische Formeln kommen bei gebrochenrationalen Funktionen relativ häufig vor, daher bitte unbedingt vorher ansehen! Sie haben den Vorteil, dass man – weges des Satzes vom Nullprodukt – sofort ablesen kann, für welche Zahlen die Gleichung null wird. Alternativ kann man die quadratische Gleichung auch wie gewohnt lösen:
Die Funktion ist also bei −2 und 2 nicht definiert:
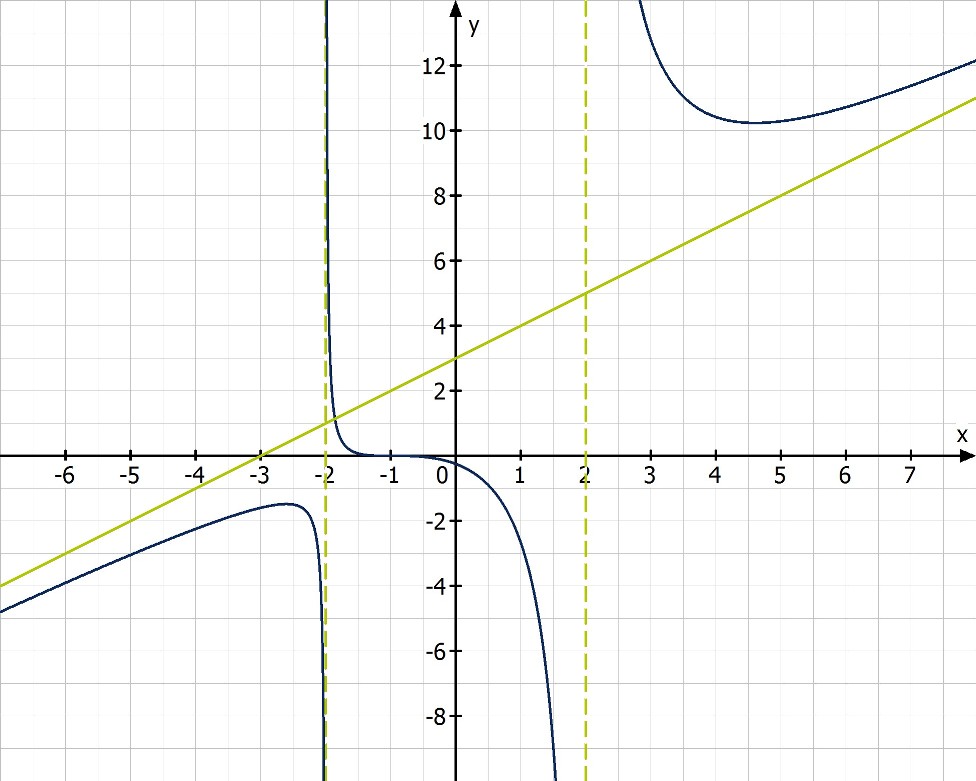
Da die Zählerfunktion an diesen Stellen ungleich null ist, handelt es sich um Polstellen. Das heißt, es gibt zwei senkrechte Asymptoten.
2. Schnittpunkte mit den Achsen
Die Schnittpunkte mit den Achsen findet man, indem man den Funktionswert an der Stelle x = 0 ermittelt (Schnittpunkt mit der y-Achse) …
also
… und die Zählerfunktion gleich null setzt (Schnittpunkt(e) mit der x-Achse):
Da die Zählerfunktion den Grad 3 hat und ein freies Glied (Zahl ohne x), kann man die Gleichung nicht durch Ausklammern vereinfacht lösen, sondern nur durch Polynomdivision oder Horner-Schema den Grad der Funktion um eins verringern. Für beide Verfahren muss man die erste Nullstelle durch Ausprobieren ermitteln:
Die erste Nullstelle ist also bei . Man teilt daher durch den Linearfaktor:
Das Horner-Schema würde wie folgt aussehen:
| 2 | 6 | 6 | 2 | |
| 0 | −2 | −4 | −2 | |
| x1 = −1 | 2 | 4 | 2 | 0 |
Weiter geht es dann entweder mit der abc-Formel: , nach Normierung mit der pq-Formel oder man erkennt eine binomische Formel:
In diesem Beispiel ist x1,2,3 = −1 eine dreifache Nullstelle.
3. Verhalten in der Nähe der Polstellen
Nun untersucht man das Verhalten links- und rechtsseitig der Polstellen:
Setzt man eine etwas kleinere Zahl als −2 für x in die Funktionsgleichung ein, ist der Funktionswert negativ. Eine etwas größere Zahl als −2 ergibt einen positiven Funktionswert, d.h. hier liegt eine Polstelle mit Vorzeichenwechsel von – nach + vor.
Annäherung von links an x = −2:
Annäherung von rechts an x = −2:
Setzt man eine etwas kleinere Zahl als 2 für x in die Funktionsgleichung ein, ist der Funktionswert negativ. Eine etwas größere Zahl als 2 ergibt einen positiven Funktionswert, d.h. auch hier liegt eine Polstelle mit Vorzeichenwechsel von – nach + vor.
Annäherung von links an x = 2:
Annäherung von rechts an x = 2:
4. Randverhalten
Es fällt direkt ins Auge, dass der Grad des Zählers (hoch 3) um eins größer ist, als der Nennergrad (hoch 2). Das lässt erwarten, dass sich der Graph der Funktion für größer bzw. kleiner werdende x einer Geraden nähert.
Um die Gleichung der Asymptote zu ermitteln, teilt man die Zählerfunktion mittels Polynomdivision durch die Nennerfunktion:
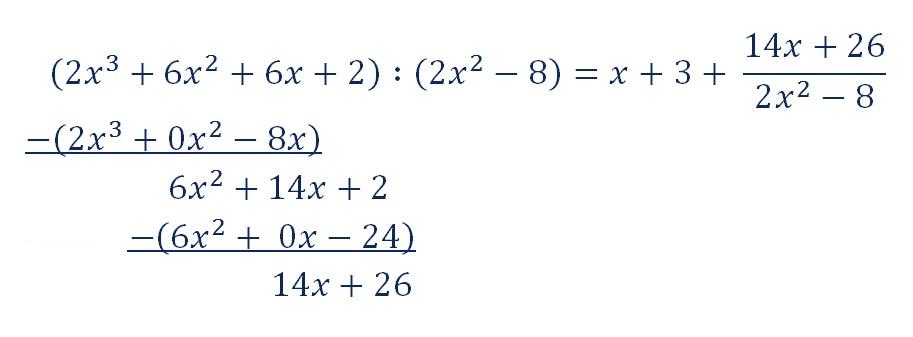
Der ganzrationale Teil bildet die Gleichung der schrägen Asymptote:
5. Extrempunkte
Um zuerst einmal die Extremstellen berechnen zu können, braucht man die erste Ableitung der Funktion.
Egal welche Darstellungsform man zum Bilden der Ableitungsfunktionen lieber nimmt, man kommt um die Quotientenregel nicht herum. Sie lautet in der Kurzschreibweise:
Zu Beginn legt man am besten eine kleine Tabelle an und setzt danach die Teile entsprechend der Vorschrift zusammen. Damit das spätere Vereinfachen leichter fällt, kann man gleich mit den faktorisierten Formen rechnen.
| Funktionen | Ableitungen | |
| Zähler | u | u‘ |
| Nenner | v | v‘ |
| Nenner² | v² | |
| |
||
Wie bei der Kurvendiskussion einer ganzrationalen Funktion lautet die notwendige Bedingung für Extremstellen:
Bei einer gebrochenrationalen Funktion reicht es aus, den Zähler gleich null zu setzen:
Auch die Lösung dieser Gleichung beginnt man entweder mit einer Polynomdivision oder dem Horner-Schema. Man erhält folgende Ergebnisse:
s
Anschließend untersucht man entweder die erste Ableitung auf Vorzeichenwechsel oder berechnet für die gefundenen Stellen die Funktionswerte der zweiten Ableitung. Erst, wenn sowohl die notwendige als auch die hinreichende Bedingung
und!
erfüllt ist, handelt es sich tatsächlich um eine Extremstelle! Da man die zweite Ableitung auch zur Berechnung von Wendestellen braucht, zieht man diesen Weg meist dem anderen vor.
ist kleiner als 0
ist größer als 0
Man erkennt, dass die Funktion zwei Extremstellen und einen Sattelpunkt hat. Die Koordinaten des Hoch- und Tiefpunktes erhält man durch Einsetzen der Ergebnisse in die Ausgangsfunktion.
6. Graph
Und so sieht der Graph der Funktion aus: