Gleichungssysteme mit zwei Variablen
Das Lösen von Gleichungen mit einer Variablen stellt in der Regel keine große Herausforderung dar. Kommt jedoch eine zweite hinzu, wird es komplizierter. Das liegt u.a. daran, dass man sowohl im Unterricht als auch in Mathebüchern verschiedenen Vorgehensweisen begegnet.
Praxisbeispiel:
Ein Softdrink und vier Döner kosten zusammen 16 €. Drei Softdrinks und zwei Döner kosten 13 €. Wie viel kostet ein Softdrink und wie viel ein Döner?
Der Übersichtlichkeit halber macht es bei solchen Aufgaben Sinn, zuerst eine Tabelle anzulegen. Das, was gesucht – und damit unbekannt ist – bezeichnet man z.B. mit x und y. In diesem Beispiel soll x der Preis für einen Softdrink und y der Preis für einen Döner angeben. Dann sollte man wissen, dass gilt: Preis • Menge = Kosten. Die Tabelle gestaltet sich wie folgt:
| Softdrink | Döner | Gesamtkosten | ||
| 1⋅x | 4⋅y | 16 | ||
| 3⋅x | 2⋅y | 13 |
Die beiden Gleichungen sind damit eigentlich schon gefunden, denn es müssen nur noch die richtigen Rechenzeichen eingesetzt werden:
Zur Lösung eines solchen linearen Gleichungssystems mit zwei Variablen lernt man in der Schule drei Verfahren:
Merke: Ziel aller drei Verfahren ist, erst die eine, dann die andere Variable stufenweise zu bestimmen.
1. Einsetzungsverfahren
Aus der ersten Gleichung erhält man durch Termumformung:
Jetzt weiß man zwar immer noch nicht, welchen Wert y annimmt, aber den Wert für x kann man als Differenz von 16 minus dem Vierfachen dieser Zahl ansehen. Daher setzt man diesen Term anstelle von x in die andere Gleichung ein – aber Achtung, der Term muss in eine Klammer geschrieben werden!
Klammer ausmultiplizieren, Gleiches zusammenfassen und Gleichung wie gewohnt durch Äquivalenzumformungen lösen:
|
|
Damit wäre der Dönerpreis mit 3,50 € gefunden, bleibt noch der Preis für einen Softdrink auszurechnen:
Bei einer anderen Schreibweise rechnet man zwar dieselben Schritte, es werden aber immer beide Gleichungen aufgeschrieben:
| 1. | Die 1 vor dem x wurde weggelassen. | |
| 2. | Die erste Gleichung wurde nach x aufgelöst und dieser Term in die zweite eingesetzt. | |
| 3. | Die erste Gleichung blieb unverändert, bei der zweiten wurde die Klammer ausmultipliziert. | |
| 4. | Die erste Gleichung blieb unverändert, die zweite Gleichung wurde vereinfacht. | |
| 5. | Die erste Gleichung blieb unverändert, die zweite wurde nach y aufgelöst. | |
| 6. | Der Term für y wurde in die erste Gleichung eingesetzt. Die zweite blieb unverändert. | |
| 7. | Die erste Gleichung zeigt das Ergebnis für x. Die zweite das Ergebnis für y. |
2. Gleichsetzungsverfahren
Um das Gleichungssystem mit dem Gleichsetzungsverfahren lösen zu können, muss auf einer Seite der Gleichungen dasselbe stehen:
| 1. | ||
| 2. | Die Gleichungen wurden so umgeformt, dass die Variable x auf einer Seite alleine steht. | |
| 3. | Die erste Gleichung wurde mit 3 multipliziert, damit bei beiden Gleichungen auf der linken Seite dasselbe steht. | |
| 4. | Die erste Gleichung wurde aus 2. übernommen, in der zweiten Zeile wurden die rechten Seiten einander gleichgesetzt. | |
| 5. | Die erste Gleichung blieb unverändert. Die zweite wurde umgeformt. | |
| 6. | Die erste Gleichung blieb unverändert. Die zweite wurde nach y aufgelöst und umgestellt. | |
| 7. | Der Term für y wurde in die erste Gleichung eingesetzt. Die zweite blieb unverändert. | |
| 8. | Die erste Gleichung zeigt das Ergebnis für x. Die zweite das Ergebnis für y. |
Dieses Verfahren macht nur dann wirklich Sinn, wenn auf einer Seite der beiden Gleichungen – wie bei Schritt 3 – bereits dasselbe steht. Dann kann man einfach die beiden anderen Seiten einander gleichsetzen, da sie ja beide denselben Wert haben. Das geht auch so:
Die Lösung setzt man nun in eine der Gleichungen anstelle von y ein, sie muss beide Gleichungen erfüllen:
| in 1. Gleichung oder | in 2. Gleichung |
|
|
3. Additionsverfahren
Beim Additionsverfahren versucht man durch Addition (oder Subtraktion) beider Gleichungen eine Variable herausfallen zu lassen. Das wiederum ist nur dann möglich, wenn ein Term denselben Betrag hat:
| 1. | Es wurde darauf geachtet, dass x und y übereinander stehen. | |
| 2. | Die zweite Gleichung wurde mit −2 multipliziert. | |
| 3. | Die erste Gleichung blieb unverändert, die zweite ist die Summe beider Gleichungen. | |
| 4. | Die erste Gleichung blieb unverändert, die zweite wurde nach x aufgelöst. | |
| 5. | In die erste Gleichung wurde der Wert für x eingesetzt. Die zweite blieb gleich. | |
| 6. | Die erste Gleichung wurde umgeformt, die zweite blieb unverändert. | |
| 7. | Die erste Gleichung wurde nach y aufgelöst, beide zeigen die Lösung. |
Schneller geht es wie folgt:
| Erste Lösung. | |
| Der Term für x wurde in die nicht umgeformte, erste Gleichung eingesetzt. |
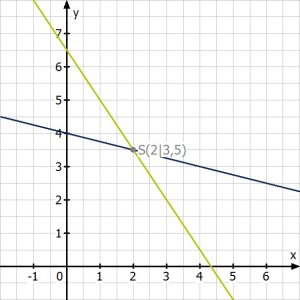
Welche Methode man wann wählen sollte, hängt davon ab, wonach gefragt ist und in welcher Form die beiden Gleichungen gegeben sind. Soll man die Lösung auch grafisch ermitteln, macht das Gleichsetzungsverfahren am meisten Sinn, denn beide Gleichungen müssen zuerst in die allgemeine Geradenform gebracht werden:
Grafisch ist die Lösung dieses LGS mit zwei Variablen der Schnittpunkt, denn es gibt nur einen Punkt, der beide Gleichungen erfüllt: