Ortskurve berechnen

Bei der Diskussion einer Funktionenschar, die zusätzlich zur Variablen noch einen oder mehrere Parameter (z.B. k oder t) enthält, wird häufig nach einer Ortskurve gefragt. Das macht insofern Sinn, da Scharen von Funktionen auch mehrere Funktionsgraphen haben, die wiederum ihre eigenen Extrem- und Wendepunkte besitzen. Eine Ortskurve ist die Funktion, die diese Punkte (Tiefpunkte, Hochpunkte oder Wendepunkte) graphisch gesehen miteinander verbindet. Hinweis: Auch wenn sie Ortskurve heißt, so kann der Graph einer solchen auch eine Gerade sein.

Gegeben ist folgende Funktionenschar mit t > 0 :

$f_t(x)=x^2-tx+\frac{1}{2}t^2$

Gesucht: Ortskurve der Tiefpunkte der Funktionenschar.

Um die Extremstellen bestimmen zu können, benötigen wir die erste Ableitung der Funktionenschar und setzen diese gleich null (notwendige Bedingung):

$f'_t(x)=2x-t=0$ Daraus folgt: $x=\frac{t}{2}$

Tipp: Anstelle des Scharparameters t kann man sich eine beliebige Zahl vorstellen (etwaige Einschränkungen beachten, hier t > 0). Daher rechnet man mit diesem Parameter, als wäre er irgendeine (positive) Zahl.

Den Beweis, dass es sich dabei tatsächlich um Extremstellen handelt, bringt erst die Untersuchung auf Vorzeichenwechsel bzw. alternativ das Einsetzen dieser Stelle(n) in die zweite Ableitung. Allerdings sollte man wissen, dass der Graph einer quadratischen Funktion der Form y = ax² + bx + c mit a > 0 eine nach oben geöffnete Parabel ist, d.h. der Scheitelpunkt kann nur ein Tiefpunkt sein. Daher sparen wir uns weitere Berechnungen an dieser Stelle.

Der zugehörige Funktionswert wird durch Einsetzen dieser Stelle in die Ausgangsfunktion berechnet:

$f_t(\frac{t}{2})=(\frac{t}{2})^2-t(\frac{t}{2})+\frac{1}{2}t^2$

Man beachte die Potenzgesetze:

$f_t(\frac{t}{2})=\frac{t^2}{4}-\frac{t^2}{2}+\frac{t^2}{2}=\frac{t^2}{4}$

Die Koordinaten der Tiefpunkte der Funktionenschar sind damit gefunden:

$T(\frac{t}{2}|\frac{t^2}{4})$

Setzt man für t zulässige Zahlen ein, erhält man für t = 1 ⇒ $T_1 (\frac{1}{2}|\frac{1}{4})$ ,
und für t = 2 ⇒ $T_2 (1|1)$ Diese Punkte müssen auf der Ortskurve liegen.

Man stellt nun die Gleichung der Extremstelle nach t um:

$x=\frac{t}{2}\Rightarrow t=2x$
und setzt dieses Ergebnis für t in die y-Koordinate ein:

$y=\dfrac{(2x)^2}{4}=\dfrac{4x^2}{4}=x^2$

Die gesuchte Ortskurve ist die Normalparabel.

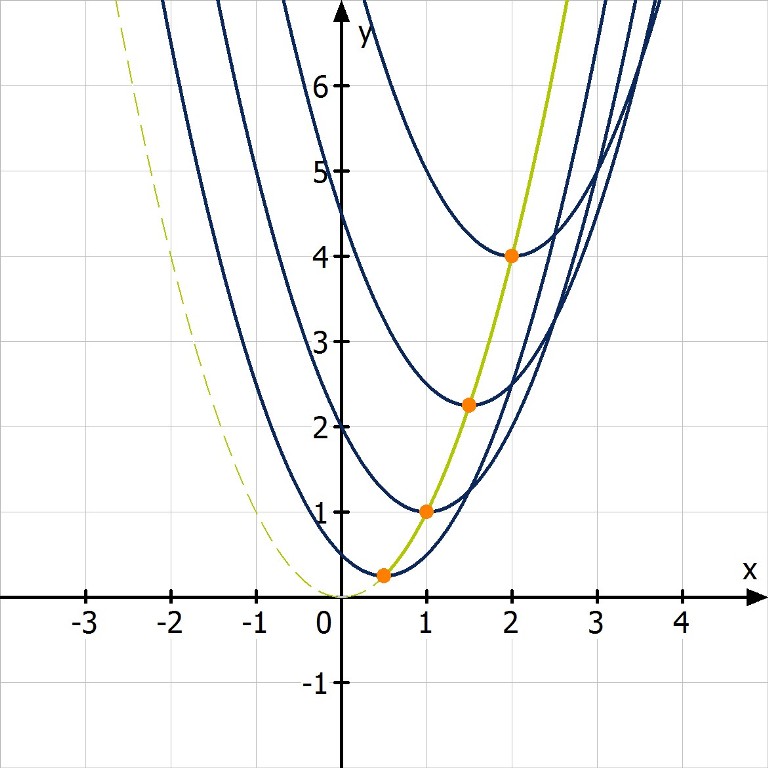
Ortskurve

Bei der Suche nach der Ortskurve der Wendepunkte rechnet man entsprechend mit den Koordinaten des Wendepunktes. Eine quadratische Funktion hat keine Wendepunkte.