Quadratische Funktionen

Eine der wohl bekanntesten quadratischen Funktionen, stellt die Flächeninhaltsfunktion eines Quadrates dar. Sie ergibt sich aus der Multiplikation der Seitenlängen, die beim Quadrat gleich lang sind:

$A(x)=x\cdot x={ x }^{ 2 }$

Setzt man für die Variable x mögliche Seitenlängen ein, dann erhält man folgende Funktionswerte:

Seitenlänge	x	0	1	2	3	4
Flächeninhalt	A(x)	0	1	4	9	16

Die Menge aller zulässigen Werte für x gibt die Definitionsmenge an. Da eine Seitenlänge nicht kleiner als null sein kann, ist diese Funktion nur für x ≥ 0 definiert.

Die einfachste Form einer quadratischen Funktion lautet:

$f(x)=x^2$

x	-4	-3	-2	-1	0	1	2	3	4
f(x)	16	9	4	1	0	1	4	9	16

Man erkennt, dass sich die Funktionswerte links- und rechtsseitig von x = 0 wiederholen. Das kommt durch die Multiplikation zweier negativer Werte, die immer zu einem positiven Ergebnis führt.

Der Graph einer quadratischen Funktion ist eine Parabel, in diesem Fall die Normalparabel:

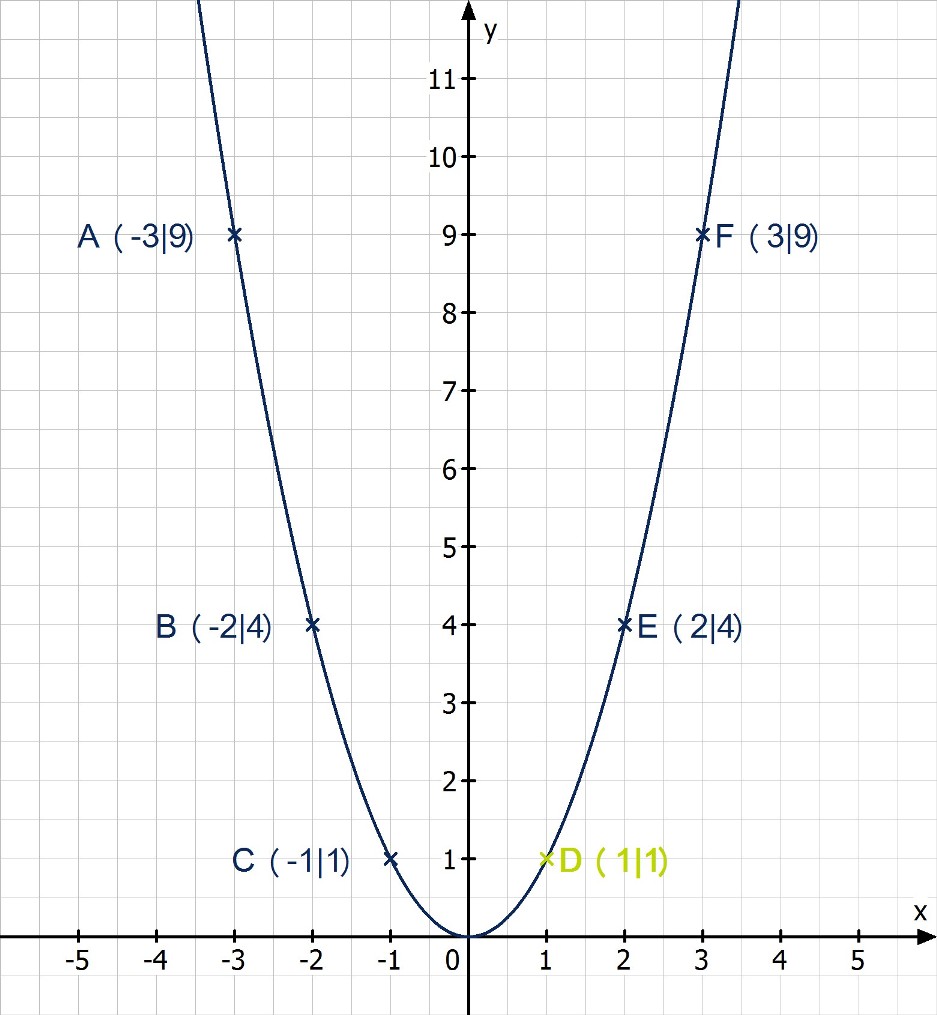
Ihr Graph verläuft kurvenförmig – erst fallend, dann steigend – wobei der tiefste Punkt, der Scheitel, im Ursprung liegt. Die Normalparabel geht durch den Punkt (1|1). Eine weitere wichtige Eigenschaft ist die Achsensymmetrie zur y-Achse.

Quadratische Funktionen können verschiedene Formen haben. Die allgemeine Form einer quadratischen Funktion lautet:

$f(x)=ax^2+bx+c$

Je nachdem, ob die Koeffizienten b oder c den Wert null haben, kann eine quadratische Funktion unterschiedlich aussehen. Lediglich a darf nicht null sein (ansonsten wäre es keine quadratische, sondern eine lineare Funktion).

a	b	c	Beispiel	Graph
1	0	0	$x^2$	Normalparabel
1	0	> 0	$x^2+3$	nach oben verschobene Normalparabel
1	0	< 0	$x^2-3$	nach unten verschobene Normalparabel
> 0	0	0	$2x^2$	nach oben geöffnete Parabel U
< 0	0	0	$-2x^2$	nach unten geöffnete Parabel ∩

\|a\|	b	c	Beispiel	Graph
> 1	0	0	$2x^2$	gestreckte (schmalere) Parabel
< 1	0	0	$0,5x^2$	gestauchte (breitere) Parabel

|a| (sprich: Betrag von a) ist immer positiv!

Je größer der Betrag von a ist, desto schmaler ist der Graph der Funktion.

Neben der Parameter– bzw. Polynomform-Schreibweise, gibt es noch die sogenannte Scheitelpunktform einer quadratischen Funktion:

$f(x)=a(x-d)^2+e$

Sie heißt so, weil man dabei die Koordinaten des Scheitelpunkts (höchster oder tiefster Punkt der Parabel) direkt ablesen kann:

$S\left( { d }\,|\,{ e } \right)$

a	d	e	Beispiel	Graph
1	> 0	0	$(x-1)^2$	um d Einheiten entlang der x-Achse nach rechts verschobene Normalparabel
1	< 0	0	$(x+1)^2$	um d Einheiten entlang der x-Achse nach links verschobene Normalparabel
1	> 0	> 0	$(x-1)^2+3$	um d Einheiten nach rechts und um e Einheiten nach oben verschobene Normalparabel
1	< 0	< 0	$(x+1)^2-3$	um d Einheiten nach links und um e Einheiten nach unten verschobene Normalparabel
> 1	> 0	> 0	$2(x-1)^2+3$	nach oben geöffnete, um den Faktor a gestreckte, nach rechts und oben verschobene Parabel

Mit einem grafikfähigen Taschenrechner, einer Mathe-App oder Plotter-Software kann man sich den Einfluss der Koeffizienten bzw. Parameter auf das Aussehen der Parabel leicht veranschaulichen.

Die folgende Abbildung zeigt einige Parabeln und deren Funktionsgleichungen:

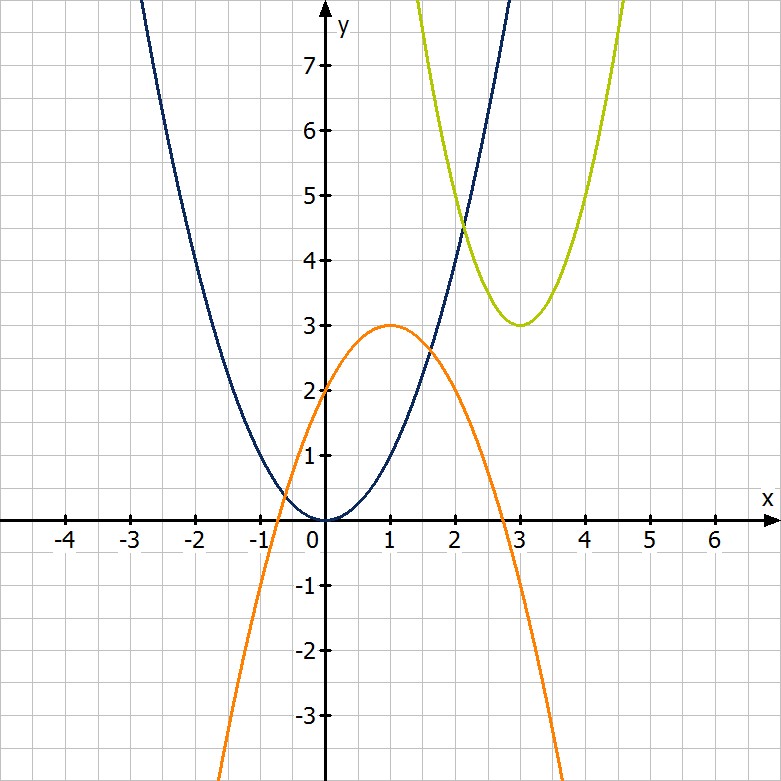Arten von Parabeln blau: $f(x)=x^2$ mit $S\left( { 0}\,|\,{ 0 } \right)$
orange: $f(x) =-(x-1)^2+3$ mit $S\left( { 1 }\,|\,{ 3 } \right)$
grün: $f(x)=2(x-3)^2+3$ mit $S\left( { 3 }\,|\,{ 3 } \right)$