Lage von Geraden und Ebenen

Im dreidimensionalen Raum können Geraden und Ebenen verschieden angeordnet sein, sodass man folgende Möglichkeiten von Lagebeziehungen unterscheidet:

  • parallel
  • identisch bzw. enthalten
  • schneidend
  • orthogonal
  • windschief

Für eine Geradengleichung in Parameterform bzw. Punkt-Richtungsform braucht man einen Punkt der Geraden als Stützvektor und einen Richtungsvektor, den man sich auch aus zwei Punkten der Geraden (als Verbindungsvektor) errechnen kann:

g\!:\vec{x}=\vec{p}+r\cdot\vec{u}

Für eine Ebenengleichung in Parameterform bedarf es ebenfalls mindestens eines Punktes der Ebene als Stützvektor und entweder …
a) zweier linear unabhängiger (nicht paralleler) Richtungsvektoren, die in der Ebene liegen und diese aufspannen. Auch diese Spannvektoren können als Verbindungsvektoren des Stützvektors zu zwei anderen Punkten der Ebene gewonnen werden:

E\!:\vec{x}=\vec{p}+s\cdot\vec{u}+t\cdot\vec{v}

oder
b) eines Punktes der Ebene als Stützvektor und eines orthogonal zur Ebene stehenden Normalenvektors:

E\!:(\vec{x}-\vec{p})\cdot\vec{n}=0

In der Abbildung wurde der Punkt A mit \vec{p}=\vec{a} als Stützvektor gewählt:

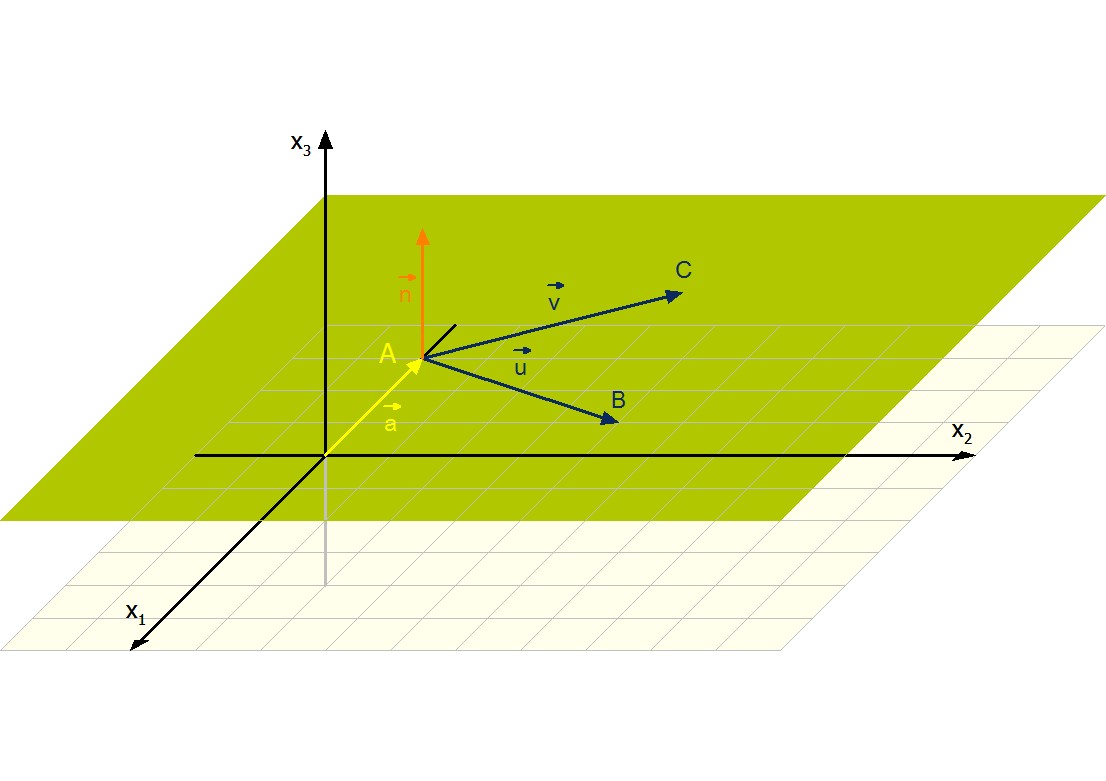EbenengleichungMöchte man nun herausfinden, wie Geraden und Ebenen zueinander stehen, müssen verschiedene Schritte unternommen werden.

Um die gegenseitige Lage zweier Geraden zu untersuchen, setzt man i.d.R. die jeweiligen Gleichungen gleich. Man erhält ein lineares Gleichungssystem (kurz: LGS), das entweder keine, unendlich viele oder genau eine Lösung hat. In den beiden Fällen keiner Lösung, kommt es auf die Richtungsvektoren an.

Man kann auch zuerst den Test auf Parallelität machen. Wenn die beiden Geraden parallel sind, dann ist der eine Richtungsvektor ein Vielfaches des anderen Richtungsvektors. Aber dann könnten beide Geraden immer noch identisch sein. Das überprüft man mit der sogenannten Punktprobe. Gibt es auch einen gemeinsamen Punkt, dann muss es sich um dieselbe Gerade handeln.

Kann man Parallelität ausschließen, können sich die zwei Geraden nur noch schneiden oder zueinander windschief sein. Man untersucht dann, ob das LGS eine eindeutige oder keine Lösung hat.

Lage Gerade g zu Gerade h LGS:
g = h
parallel Die Richtungsvektoren sind Vielfache voneinander. keine Lösung
identisch Die Richtungsvektoren sind Vielfache voneinander
und die Punktprobe ist positiv.		 unendlich viele Lösungen
schneidend Es gibt ein s und ein t, welches alle drei Gleichungen erfüllt. Der Schnittpunkt S ergibt sich durch Einsetzen von s oder t in eine der Geradengleichungen. eine Lösung
windschief Es gibt kein s und kein t, welches alle drei Gleichungen erfüllt. keine Lösung

Auch die Lage einer Geraden zu einer Ebene wird durch die Lösung eines LGS bestimmbar:

  • Liegt die Ebene in Parameterform vor, setzt man beide gleich. Man erhält drei Gleichungen mit drei Variablen. Für den Fall einer eindeutigen Lösung, braucht man nur noch den Parameter der Geraden in die Geradengleichung einsetzen. Man erhält damit den Schnittpunkt von Gerade und Ebene (Durchstoßpunkt).

Alternativ könnte man auch zuerst die Parametergleichung in eine Koordinatengleichung umrechnen und dann wie folgt weitermachen …

  • Ist die Ebene in Koordinatenform gegeben, kann man x1, x2, x3 aus der Geradengleichung direkt in die Ebenengleichung einsetzen und gewinnt damit den Parameter der Geradengleichung.
  • Bei einer Ebene in Normalenform setzt man ebenfalls x1, x2 und x3 aus der Geradengleichung ein. Das Ausmultiplizieren des Skalarprodukts ergibt den Parameter.
Lage Gerade g zu Ebene E (E in Normalenform) LGS:
g = E
parallel Der Richtungsvektor der Geraden steht senkrecht zum Normalenvektor. Das Skalarprodukt ist null. keine Lösung
enthalten Der Richtungsvektor der Geraden steht senkrecht zum Normalenvektor. Das Skalarprodukt ist null und die Punktprobe ist positiv. unendlich viele Lösungen
schneidend Der Richtungvektor der Geraden steht nicht senkrecht auf dem Normalenvektor. Das Skalarprodukt ist ungleich null. eine Lösung

 Fortsetzung folgt!

Nach oben