Lineare Funktionen
Eine Funktion ist eine eindeutige Zuordnung, bei der jedem x genau ein y zugeordnet wird. Du hast vielleicht schon proportionale Zuordnungen kennengelernt:
| Anzahl Personen | Gesamtpreis für Kinokarten in Euro |
| 0 | 0 |
| 1 | 9 |
| 2 | 18 |
| 3 | 27 |
| x | y = x • 9 = 9x |
Eindeutig bedeutet: Es kann für eine bestimmte Anzahl Personen nur einen bestimmten Preis geben, nicht zwei verschiedene. Es darf also in der Tabelle immer nur eine Zahl auf der linken und eine auf der rechten Seite stehen.
Die Zuordnungsvorschrift, mit der man den Gesamtpreis für jede beliebige Anzahl von Personen berechnen könnte, lautet demzufolge:
Eine proportionale Funktion ist eine spezielle, lineare Funktion. Ihr Graph geht immer durch den Ursprung. Die allgemeine Form einer proportionalen Funktion lautet:
f(x) bedeutet: Funktionswert an der Stelle x
Die allgemeine Form einer linearen Funktion lautet:
Die Graphen linearer Funktionen sind Geraden:

Die Geraden lassen sich auch ohne Wertetabelle zeichnen. Das geht recht einfach, wenn man sich überlegt, was z.B. x = 0 graphisch bedeutet. Das sind alle Punkte, die auf der y-Achse liegen, also der Schnittpunkt mit der y-Achse. Setzt man in eine lineare Funktion für die unabhängige Variable x die Zahl 0 ein, so bleibt immer das b übrig:
In der Praxis hat das Absolutglied b die Bedeutung einer fixen Komponente bzw. es gibt den Anfangswert an. Das kann beim Handytarif die Grundgebühr sein oder wenn es um Veränderung im Zeitverlauf geht, die Startposition. Du fragst danach mit der Frage: „Wie viel war zu Beginn?“
In der Regel schneidet eine Gerade auch die x-Achse. Diese Stelle nennt man Nullstelle. Der Schnittpunkt mit der x-Achse ist diejenige Stelle, für die gilt:
Sobald man zwei Punkte einer Geraden kennt, kann man sie zeichnen. Aber es gibt noch eine einfachere Möglichkeit, die sich genau diesen Zusammenhang zunutze macht: Wenn man sich anschaut, wie man von dem Punkt auf der y-Achse zur Nullstelle kommt:
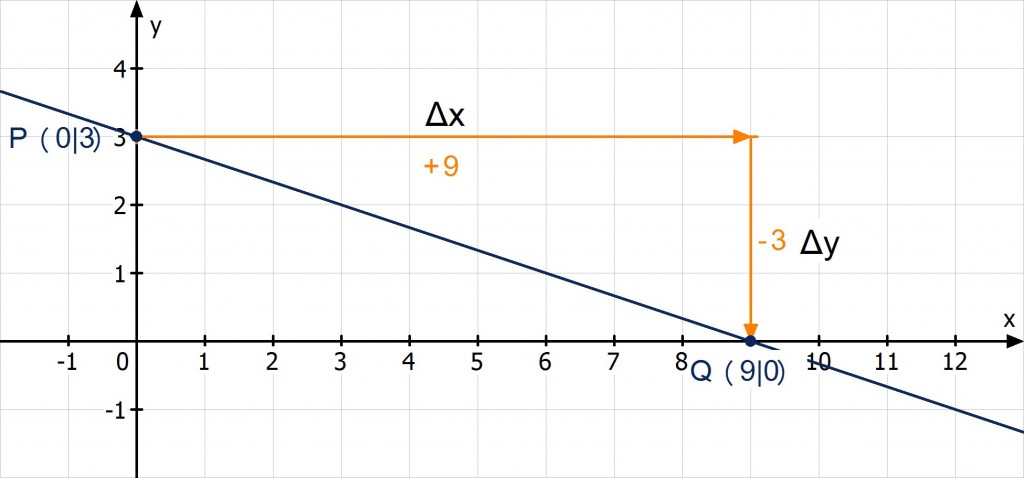
In diesem Fall eine streng monoton fallende Gerade, die die y-Achse im Punkt P (0|3) und die x-Achse im Punkt Q (9|0) schneidet. Es gibt Straßen, die so steil bergab gehen oder man könnte sich diese Gerade auch als eine Anlaufschanze vorstellen.
Von P nach Q geht es insgesamt auf einer Strecke von 9 Einheiten, 3 Einheiten nach unten. Das Schöne an dieser Darstellung ist, dass man das b für die Geradengleichung direkt ablesen kann und sich auch die Steigung recht einfach berechnen lässt. Wir nehmen …
- den Schnittpunkt mit der y-Achse (b) als eine Art Startposition:
und berechnen - die Steigung (m), die als Quotient aus Höhenunterschied und Horizontalunterschied (Entfernung der beiden Punkte voneinander) definiert ist:
Die erste Darstellungsform nennt man Punkt-Steigungs-Form, die zweite ist die sogenannte Zwei-Punkte-Form. Es ergibt sich in diesem Beispiel für die Steigung m:
Und damit kennt man die Funktionsvorschrift der hier abgebildeten linearen Funktion:
Soll man eine solche Funktion ohne Wertetabelle zeichnen, gibt der Nenner des Steigungsbruchs die Anzahl der Einheiten, die man vom y-Achsenabschnitt nach rechts geht und der Zähler die Anzahl der Einheiten, die man nach oben oder unten geht, an. Ist m eine ganze Zahl, geht man immer eine Einheit nach rechts. Bei positivem m, ist auch die Steigung positiv. Hat m ein negatives Vorzeichen – wie hier – ist die Steigung negativ.
Fortsetzung folgt!
