Rechnen mit negativen Zahlen
In der Grundschule rechnet man mit natürlichen Zahlen. Natürlich ist, dass eine Kuh eine ganze Kuh ist (denn es leben keine halben Kühe). Ein Ganzes ist also eine in sich geschlossene Einheit. So kannst du dir sicher spielend vorstellen was es bedeutet, wenn man von drei Bonbons eines isst. Dann bleiben noch zwei Bonbons übrig. Um den Rest zu berechnen, zieht man von einer positiven ganzen Zahl eine andere, kleinere ab:
1. Addition und Subtraktion
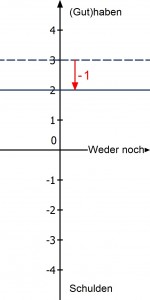
Das geht noch prima. Was aber, wenn man nur ein Bonbon hat und mit zwei Freunden zusammen ist, die auch eines wollen. Dann bräuchte man eigentlich drei, hat aber nur eines. Das heißt, es fehlen zwei. Den Zustand des Fehlens drückt man mit einem negativen Vorzeichen aus:
a) Zustand – Änderung – Zustand
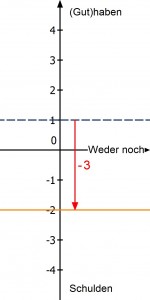
Wenn es ums Geld geht, ist ein negatives Vorzeichen vor einer Zahl auf dem Kontoauszug wirklich negativ (im Sinne von „schlecht“), denn dann hat man mehr ausgegeben als man eigentlich hatte und damit Schulden bei der Bank. Du kennst sicher den Fall, dass du dir schon mal Geld von deinen Freunden leihst. Guthaben ist dagegen das Geld, das du tatsächlich hast. Kannst du das geliehene Geld nur langsam abstottern, werden die Schulden zwar weniger, aber es bleiben Schulden: 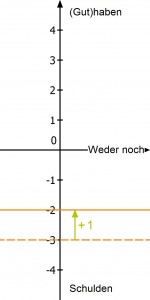
Wenn du deine Schulden ganz abbezahlst und noch mehr, hast du wieder ein Guthaben. Das könnte sich wie folgt darstellen: 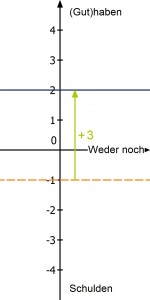
In den beiden nächsten Fällen würdest du noch mehr Schulden machen: bzw.
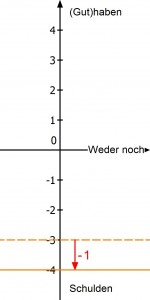
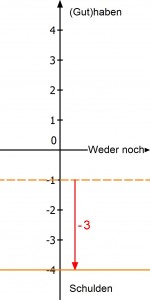
In all diesen Fällen gibt das Vorzeichen einen bestimmten Zustand an, das Rechenzeichen eine Zustandsveränderung (Richtung des Pfeils).
b) Änderung – Änderung – Änderung
Man kann aber auch die Zeichen vor einer Zahl als Änderung ansehen und das Rechenzeichen als Verknüpfung derselben. Das Ergebnis gibt dann die Gesamtänderung an. Dieses Wissen braucht man bei diesem Beispiel: 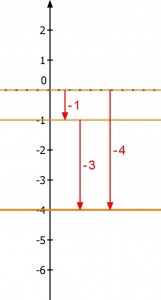
Was dasselbe besagt wie im Beispiel zuvor: Du gibst ein Euro mehr aus, als du hast – das sind ein Euro Schulden – und verschuldest dich um weitere drei Euro. Somit müssen die Schulden dem Betrag nach größer werden.
Zur Erinnerung:
Auch dieses Rechenbeispiel würde dasselbe Ergebnis liefern:
- weil man ein positives Vorzeichen generell weglassen kann,
- weil man jede Subtraktion als eine Addition mit der Gegenzahl schreiben kann.
Treffen also ein Minuszeichen und ein Pluszeichen zusammen, setzt sich das Minuszeichen durch!
Die Tabelle zeigt die wesentlichen Kombinationen, denen man begegnen kann. Da bei der Addition das Kommutativgesetz gilt, ist die Reihenfolge bei Summanden egal. Und da man jede Subtraktion in eine Addition mit der Gegenzahl umwandeln kann, reduziert sich das Ganze nochmals.
| (+3) | − | (–1) | = | (+3) | + | (+1) | = | 3 | + | 1 | = | 4 |
| (+3) | − | (+1) | = | (+3) | + | (–1) | = | 3 | − | 1 | = | 2 |
| (–3) | − | (–1) | = | (–3) | + | (+1) | = | –3 | + | 1 | = | –2 |
| (–3) | − | (+1) | = | (–3) | + | (–1) | = | –3 | − | 1 | = | –4 |
| (+1) | − | (–3) | = | (+1) | + | (+3) | = | 1 | + | 3 | = | 4 |
| (+1) | − | (+3) | = | (+1) | + | (–3) | = | 1 | − | 3 | = | –2 |
| (–1) | − | (–3) | = | (–1) | + | (+3) | = | –1 | + | 3 | = | 2 |
| (–1) | − | (+3) | = | (–1) | + | (–3) | = | –1 | − | 3 | = | –4 |
Schaut man sich nun die grünen Spalten genauer an, erkennt man folgende Zusammenhänge:
- bei gleichen (Vor)zeichen bildet man die Summe der Beträge. Das Ergebnis hat das gemeinsame Vorzeichen.
- bei unterschiedlichen (Vor)zeichen bildet man die Differenz der Beträge. Das Ergebnis hat dann das Vorzeichen der Zahl mit dem größeren Betrag.
2. Multiplikation und Division
Bei der Multiplikation (und Division) gelten ähnliche Regeln:
- bei einer geraden Anzahl von negativen Vorzeichen ist das Produkt stets positiv – da minus mal minus plus ergibt.
- bei einer ungeraden Anzahl von negativen Vorzeichen ist das Produkt negativ – da minus mal plus minus ergibt.
| (+3) | · | (+1) | = | 3 | ||||||||||
| (–3) | · | (–1) | = | 3 | ||||||||||
| (+3) | · | (–1) | = | –3 | ||||||||||
| (–3) | · | (+1) | = | –3 | ||||||||||
| (+3) | · | (–1) | · | (+2) | = | –6 | ||||||||
| (–3) | · | (–1) | · | (+2) | = | 6 | ||||||||
| (–3) | ⋅ | (–1) | ⋅ | (–2) | ⋅ | (–4) | = | 24 |
Fortsetzung folgt!