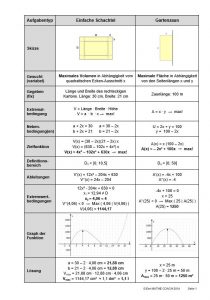
Extremwertaufgaben
Bei Extremwertaufgaben geht es um Optimierung. Man möchte z.B. wissen, bei welcher Menge der Gewinn am größten (maximal) ist oder die Kosten am niedrigsten (minimal) sind. Wer bereits den Ableitungsbegriff kennt und verschiedene Funktionstypen ableiten kann, wird bald den Sinn und Zweck des Ganzen erkennen. Mithilfe der Differenzialrechnung lassen sich nämlich Extremstellen bzw. Extrempunkte exakt und direkt berechnen. Das kommt daher, weil die Ableitungsfunktion die Steigung der Tangente an einer bestimmten Stelle des Funktionsgraphen angibt und diese nur dort gleich null ist, wo es weder bergauf noch bergab geht (→ Ableitung).
Die notwendige Bedingung für Extremstellen lautet daher:
Stellt man sich den Graphen einer Funktion z.B. als eine Art Achterbahn vor, dann gibt es neben Anfang und Ende der Strecke (Randextrema) sowohl globale/absolute als auch lokale/relative Extrempunkte: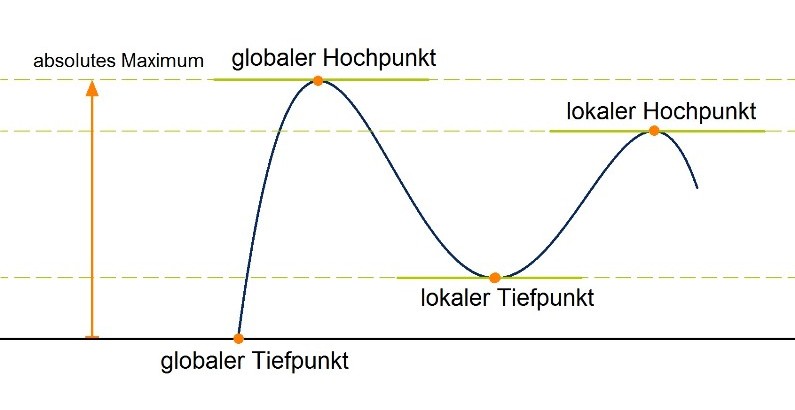 Bei der Berechnung des Extremwertes interessiert uns in erster Linie der globale Hoch- oder Tiefpunkt. Das ist der höchste bzw. tiefste Punkt der Strecke. Er ist deshalb so interessant, weil dort der Funktionswert am größten oder kleinsten ist. Gesucht wird also der größte oder kleinste Wert (Extremwert) innerhalb eines gegebenen Intervalls und/oder der Definitionsmenge.
Bei der Berechnung des Extremwertes interessiert uns in erster Linie der globale Hoch- oder Tiefpunkt. Das ist der höchste bzw. tiefste Punkt der Strecke. Er ist deshalb so interessant, weil dort der Funktionswert am größten oder kleinsten ist. Gesucht wird also der größte oder kleinste Wert (Extremwert) innerhalb eines gegebenen Intervalls und/oder der Definitionsmenge.
Die Anwendungsmöglichkeiten sind geradezu grenzenlos: In der Schule reichen sie vom miniminalen Verpackungsmaterialverbrauch bis hin zum größtmöglichen Gewinn. Daher werden zum Lösen von Extremwertaufgaben, neben dem eigentlichen Handwerkzeug einer Kurvendiskussion, auch wieder Grundlagen der Geometrie und Finanzmathematik benötigt.
Vorgehensweise:
- Analyse der Aufgabe (was soll, wie, extremal sein?).
- Vorläufige Zielfunktion aufstellen (Haupt- oder Extremalbedingung mit ein oder mehreren Variablen).
- Nebenbedingung(en) aufstellen (was ist sonst noch gegeben bzw. fix und zu beachten?).
- Nebenbedingung(en) nach einer Variablen auflösen.
- Zielfunktion mit einer Variablen aufstellen (Nebenbedingung(en) in Hauptbedingung einsetzen).
- Sinnvollen Definitionsbereich bestimmen.
- Zielfunktion ableiten und diese gleich null setzen (notwendige Bedingung zur Bestimmung von lokalen/relativen Extrema).
- Extremwerte auf das Vorliegen eines Maximums oder Minimums untersuchen.
- Lokale/relative Extremwerte mit Randextrema vergleichen (dazu auch die.Funktionswerte der Randstellen des Intervalls berechnen).
- Ergebnisse unter Beachtung des Definitionsbereichs interpretieren und sinnvolle Lösung im Sinne der Zielsetzung auswählen.
- Optimale Kombination angeben.
Schülern fällt i.d.R. das Aufstellen der Zielfunktion am schwersten, denn dafür braucht man geeignete Nebenbedingungen, die man sich manchmal erst erarbeiten muss. Ich widme mich daher im folgenden Fallbeispiel besonders diesem Aspekt.
Fallbeispiel:
Gesucht ist der größtmögliche Flächeninhalt eines Rechtecks innerhalb eines kurvigen Bereichs. Meist handelt es sich dabei um ein Rechteck, das zwischen Funktionsgraph und Achse hineinpassen soll. Sagen wir, der Besitzer einer Tennishalle möchte ein möglichst großes Schaufenster in die parabelförmige Seitenwand seiner Sportstätte einbauen lassen. Die Aufgabe könnte man wie folgt darstellen:
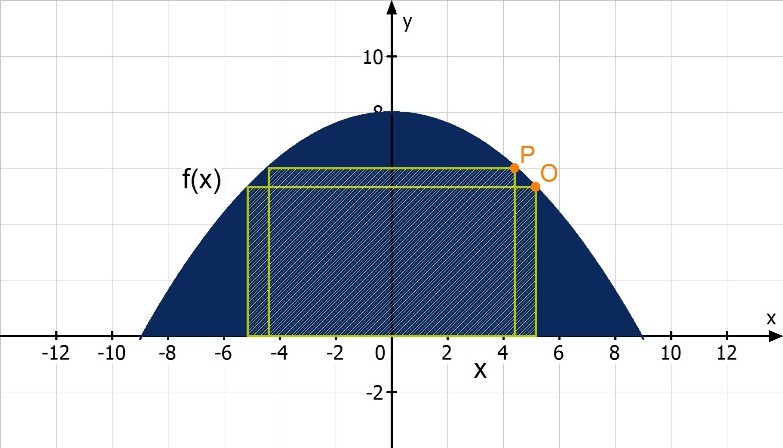
Zuerst bedarf es der Formel, mit der man den Flächeninhalt eines Rechtecks berechnen kann:
und natürlich brauchen wir die Funktion, die den Verlauf des Daches beschreibt:
Die Breite (man betrachtet zur Vereinfachung nur die rechte, positive Seite) ist x und die Höhe y. Sie ergibt sich aus dem Funktionswert an dieser Stelle. Ein mögliches Rechteck hätte also mit dem Funktionsgraphen den Punkt P gemeinsam, ein anderes den Punkt O. Ohne die Differenzialrechnung wäre es sehr mühsam, alle möglichen Kombinationen auszurechnen. Wir formulieren die vorläufige Zielfunktion:
Diese Funktion für die zu optimierende Fläche hat noch zwei Variablen. Um eine Funktion mit einer Variablen zu erhalten, setzt man den Term für y (Nebenbedingung) in die Hauptbedingung ein. Man erhält somit die reduzierte Zielfunktion A(x):
Nun sollte man sich Gedanken über das Intervall bzw. den sinnvollen Definitionsbereich machen. Wenn x gleich null oder so groß wie die halbe Seitenwand ist, entsteht überhaupt keine Fläche. Noch größere x liegen außerhalb des Möglichen. Wer die Nullstellen berechnet, erhält auch den rechten Rand des Intervalls:
Die Extremwertsuche beginnt mit der Ableitung der Zielfunktion:
Man setzt sie gleich null (notwendige Bedingung für Extrema):
und löst die Gleichung nach x auf:
Es ist noch zu prüfen, ob diese Stelle im Definitionsbereich liegt und ob es sich tatsächlich um ein Maximum handelt. Da x > 0 sein muss, kann nur das positive Ergebnis eine Lösung sein.
Man erhält die optimale Fenstergröße, indem man auch noch y ausrechnet. Die größtmögliche Fläche mit ca. 55 m² hat das Schaufenster demzufolge dann, wenn es 10,32 m breit und 5,33 m hoch ist.