Kurvendiskussion

Einen großen Teil der Oberstufe beschäftigt man sich mit Kurven. Viele Dinge unseres Lebens zeichnen sich durch einen kurvigen Verlauf aus. Die Abbildung zeigt z.B. zwei Kamelhöcker und den gekrümmten Verlauf des Graphen einer ganzrationalen Funktion vierten Grades, der annähernd die Silhouette dieser Höcker beschreibt:

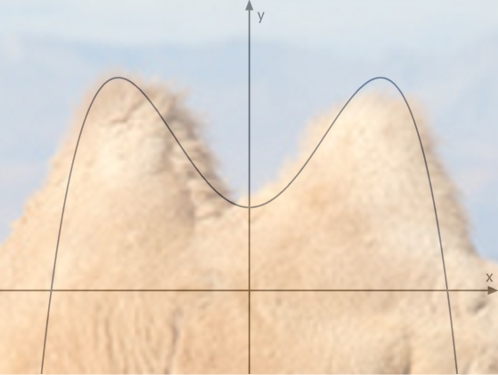
Kamelhöckerkurven

Wie man unschwer erkennen kann, sitzt man zwischen den Höckern – lokal gesehen – am tiefsten und auf den Höckern am höchsten. Mit der Differenzialrechnung lernen Schüler der Oberstufe eine Methode kennen, mit der man diese Punkte exakt bestimmen kann. Wie das geht, werde ich hier zeigen. Es ist allerdings dafür erforderlich, dass du bereits weißt, wie man eine Ableitung berechnet und was sie aussagt ->Tangentenproblem.

Bei der Diskussion einer Kurve – auch Funktionsanalyse genannt – bekommt man die Funktionsvorschrift vorgegeben, doch man weiß noch nicht, wie der Graph aussieht. Das ist dann das Ziel deiner Berechnungen: die Kurve anhand weniger charakteristischer Punkte zeichnen können. Im Fall Kamelhöcker würde das Koordinatensystem nach einer vollständigen Kurvendiskussion erst einmal so aussehen:

KV2

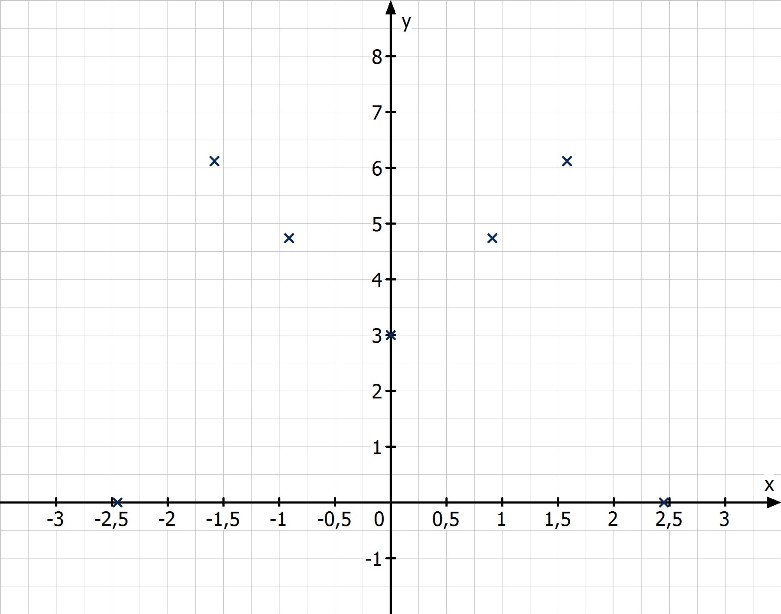
Es gehört schon ein bisschen Geschick und Erfahrung dazu, daraus eine Kurve werden zu lassen. Aber, keine Bange, mit ein paar Tricks, geht es bald leicht.

Was gehört nun zu den charakteristischen Eigenschaften dieser Funktion? Im Allgemeinen werden folgende Punkte abgearbeitet:

Defintionsbereich (Welche Zahlen sind für x zugelassen bzw. möglich?)
Symmetrie (Achsensymmetrie zur y-Achse, Punktsymmetrie zum Ursprung oder keines von beiden?)
Randverhalten bzw. Globalverlauf
Achsenschnittpunkte (y-Achsenabschnitt und Nullstellen?)
Ableitungen
Extrempunkte (Hoch- oder/und Tiefpunkte?)
Wendepunkte (Sattelpunkt?)
Wertetabelle
Graph

Beispiel: Kurvendiskussion einer ganzrationalen Funktion

Gegeben ist folgende ganzrationale Funktion:

$f(x)=-\frac{1}{2}x^4+\frac{5}{2}x^2+3$

1. Definitionsbereich

Als Erstes schauen wir uns an, für welche Zahlen diese Funktion definiert ist: $D_f=\mathbb{R}$

Das bedeutet lediglich, dass man anstelle von x jede reelle Zahl einsetzen könnte. Das sind alle Zahlen, die du bisher kennst. Bei ganzrationalen Funktionen ist das immer so. Bei gebrochenrationalen Funktionen z.B. gibt es Ausnahmen.

2. Symmetrie

Zur Symmetrie gibt es zwei einfache Fragen. Es kann nur eine Antwort zutreffen. Wenn du also bereits eine Frage bejahen konntest, dann brauchst du eigentlich den anderen Test gar nicht mehr machen. In einer Kursarbeit sollte man allerdings besser beide Tests machen oder zumindest begründen, weshalb man auf den anderen verzichtet.

Test auf Achsensymmetrie zur y-Achse:
Hat die Funktion nur gerade Exponenten? Wenn ja, spiegelt sich die eine Seite des Graphen auf der anderen Seite der y-Achse wider. Wieso das so ist, kann man mathematisch so erklären:

$f(x)=f(-x)$
$-\frac{1}{2}x^4+\frac{5}{2}x^2+3=-\frac{1}{2}(-x)^{4 }+\frac{5}{2}(-x)^2+3$
Da minus mal minus plus ergibt, ist diese Aussage wahr. Der Graph der Funktion ist also achsensymmetrisch zur y-Achse.

Test auf Punktsymmetrie zum Ursprung:
Hat die Funktion nur ungerade Exponenten und kein Absolutglied?
Dann wäre diese Aussage wahr: $f(-x)=-f(x)$
Wir beweisen, dass dem nicht so ist:

$-\frac{1}{2}(-x)^{4 }+\frac{5}{2}(-x)^2+3\ne-(-\frac{1}{2}x^4+\frac{5}{2}x^2+3)$

$-\frac{1}{2}x^4+\frac{5}{2}x^2+3\ne\frac{1}{2}x^{4 }-\frac{5}{2}x^2-3$

Aufpassen! Bei einer Minus-Klammer drehen sich die Vorzeichen in der Klammer beim Auflösen derselben um!

3. Randverhalten oder Globalverlauf

Für viele stellt sich sicher erst einmal die Frage: Was ist damit gemeint? Man möchte wissen, wie sich der Graph der Funktion mit größer oder kleiner werdendem x verhält. Geht er z.B. am rechten Rand nach oben, dann werden die Funktionswerte für immer größere Zahlen, die man in die Funktion einsetzt, auch immer größer. Oder anders gesagt: Größerer Input ergibt größeren Output. Zeigt der Graph der Funktion hingegen am rechten Rand nach unten, bedeutet es das Gegenteil:

Für $x\to+\infty$ gilt: $f(x)\to+\infty$ oder für $x\to+\infty$ gilt: $f(x)\to-\infty$

Dasselbe gibt es auch für den linken Rand der Funkton:

Für $x\to-\infty$ gilt: $f(x)\to+\infty$ oder für $x\to-\infty$ gilt: $f(x)\to-\infty$

∞ ist das Zeichen für unendlich

Es gibt noch eine andere Schreibweise (für Fortgeschrittene):

$\displaystyle\lim_{x \to\pm\infty} f(x)=\pm\infty$

lim  steht für Grenzwert

Woran erkennt man nun an der Funktion

$f(x)=-\frac{1}{2}x^4+\frac{5}{2}x^2+3$
wie ihr Graph an den Rändern aussieht? Man kann sich das Aussehen typischer Funktionen entweder merken (s. Link) oder aber, man setzt in die höchste Potenz für x zuerst -10 und dann 10 ein und rechnet die Potenz aus:

$-\frac{1}{2}(-10)^4=-5000$ und $-\frac{1}{2}(10)^4=-5000$

$10^4=10.000$ (Die Hochzahl bestimmt die Anzahl der Nullen hinter der Eins)

Wieso gerade die 10? Es könnte auch eine andere Zahl sein, die möglichst weit vom Ursprung entfernt ist. Mit Potenzen von 10 lässt es sich einfacher im Kopf rechnen. Uns interessiert ohnehin bloß das Vorzeichen des Ergebnisses. Für unsere Funktion gilt:

Für $x\to-\infty$ gilt: $f(x)\to-\infty$ und für $x\to+\infty$ gilt: $f(x)\to-\infty$

Der Graph der Funktion verläuft folglich von $-\infty\$ nach $-\infty$

4. Achsenschnittpunkte

Da es nur zwei Achsen gibt, meint man damit sowohl den Schnittpunkt mit der Ordinate (senkrechte Achse bzw. y-Achse) als auch die etwaigen Nullstellen, also mögliche Schnittpunkte mit der Abszisse (waagerechte Achse bzw. x-Achse).

Schnittpunkt mit der y-Achse:
Das ist irgendein Punkt an der Stelle x = 0:

$f(0)=-\frac{1}{2}\cdot0^4+\frac{5}{2}\cdot0^2+3=3$
Kleiner Tipp: Es ist immer die Zahl ohne x ansonsten 0. Für f(0) = 0 ist auch x = 0 und damit bereits eine Nullstelle gefunden. Der Graph berührt oder schneidet dann den Punkt (0|0), auch Ursprung genannt. Hier schneidet der Graph die y-Achse im Punkt:

$S_y=(0|3)$

Schnittpunkte mit der x-Achse (Nullstellen):
Um die Nullstellen einer Funktion zu finden, setzt man:

$f(x)=0$
$-\frac{1}{2}x^4+\frac{5}{2}x^2+3=0$

Da diese Gleichung nur gerade Exponenten hat, können wir sie durch Substitution von $x^2=z$ wie folgt zu einer quadratischen Gleichung vereinfachen:

$-\frac{1}{2}z^2+\frac{5}{2}z+3=0$ $\mid \quad :(-\frac{1}{2})$ bzw. $\cdot(-2)$

$z^2-5z-6=0$

Jetzt nur noch pq-Formel anwenden. Aufpassen! p = – 5; q = – 6:

$z_{1,2}=-\frac{p}{2}\pm\sqrt { \left( \frac { p }{ 2 } \right) ^{ 2 }-q }$

$z_{1,2}=\frac{5}{2}\pm\sqrt { \left( -\frac { 5 }{ 2 } \right) ^{ 2 }+6 }$

$z_{1,2}=\frac{5}{2}\pm\sqrt {\frac { 25 }{ 4 } +6 }$

$z_{1,2}=\frac{5}{2}\pm\sqrt {\frac { 25}{ 4 } +\frac{24}{4}}$

$z_{1,2}=\frac{5}{2}\pm\sqrt {\frac { 49 }{ 4 }}$

$z_{1,2}=\frac{5}{2}\pm{\frac { 7 }{ 2 }}$

$z_1=\frac{5}{2}+\frac { 7 }{ 2 }=\frac{12}{2}=6$

$z_2=\frac{5}{2}-\frac { 7 }{ 2 }=-\frac{2}{2}=-1$

Jetzt wird rücksubstituiert. Zur Erinnerung: $z=x^2$

$x^2=6$ $\mid \sqrt{\; }$

$x_{1,2}=\pm\sqrt{6}\approx \pm \,2{,}45$

Da man aus einer negativen Zahl keine Quadratwurzel ziehen kann, gibt es nur zwei Lösungen. Der Graph der Funktion schneidet demzufolge zweimal die x-Achse. Die Nullstellen lauten:

$N_1(-2{,}45|0)$ und $N_2(2{,}45|0)$

5. Ableitungen

Erfahrene Kurvendiskutierer beginnen eine Funktionsanalyse, indem sie gleich zu Beginn alle Ableitungen der Funktion bestimmen. Wirklich erforderlich ist es erst an dieser Stelle. Für ganzrationale Funktionen wie diese, brauchen wir neben der Potenzregel noch die Summen- und Faktorregel:

Die Summenregel besagt, dass wir die Summanden einzeln – also jedes einzelne Glied zwischen zwei Pluszeichen für sich – ableiten können und sich die Ableitungsfunktion dann aus der Summe derselben ergibt.
Nach der Faktorregel bleibt ein konstanter Faktor (die Zahl vor dem x) beim Ableiten erhalten.
Außerdem sollte man sich merken, dass das Absolutglied (der Summand ohne x) beim Ableiten komplett wegfällt.

Zur Erinnerung: Die Potenzregel für eine Funktion der Form $f(x)=x^n$ lautet:

$f'(x)=n \cdot x^{n-1}$

Beispiel: $f(x)=3x^2+x+4$ kann man auch anders schreiben:

$f(x)=3\cdot x^2+1\cdot x^1+4\cdot x^0$

$f'(x)=3\cdot2x+1$ oder
$f'(x)=2\cdot3x+1$

$f'(x)=6x+1$

Das ' Zeichen kennzeichnet die erste Ableitung

Wer sich in Bruchrechnung nicht mehr so gut auskennt, sollte sich unbedingt den verlinkten Artikel genau durchlesen! Für unser Beispiel lauten die Ableitungen:

$f(x)=-\frac{1}{2}x^4+\frac{5}{2}x^2+3$

$f'(x)=-2x^3+5x$ $\left[=4\cdot\left( -\frac { 1}{2 } \right)x^3+2\cdot\frac{5}{2}\,x\right]$

$f''(x)=-6x^2+5$

$f'''(x) =-12x$

Tipp: Mit jeder Ableitung vermindert sich der Grad der Funktion um eins! Wer seine Ableitungen überprüfen möchte, der gebe die Ausgangsfunktionen einfach hier ein: Ableitungsrechner.

6. Extrempunkte

WICHTIG! Die Ableitung gibt die Steigung des Graphen einer Funktion an einer bestimmten Stelle an. Je größer der Betrag, desto steiler die Tangente. Extrempunkte haben waagerechte Tangenten, d.h. dort ist die Steigung gleich null. Um diese Punkte zu finden, setzt man folglich die erste Ableitung gleich null. Der Mathematiker nennt dies:

notwendige Bedingung: $f'(x)=0$

$-2x^3+5x=0$ $x(-2x^2+5)=0$

Nach dem Satz vom Nullprodukt kann solch eine Gleichung nur dann wahr werden, wenn mindestens ein Faktor gleich null ist:

$x_{1}=0\quad\vee\quad-2x^2+5=0 \quad\mid \ +2x^2$

$5=2x^2\ \mid\,:\!2$

$\frac{5}{2}=x^2$ $\mid \sqrt{\; }$

$x_{2,3}=\pm\sqrt{\frac{5}{2}}\approx \pm \,1{,}58$

Es ergeben sich daraus drei mögliche Extremstellen:

$x_{E 1}=0$ , $x_{E 2}\approx-1{,}58$ , $x_{E 3}\approx 1{,}58$

Da man jetzt noch nicht weiß, ob es sich dabei um Hoch- oder Tiefpunkte handelt und es auch noch andere Ausnahmen gibt, bedarf es einer Konkretisierung:

hinreichende Bedingung:

$f'(x)=0$ und! $f''(x_{E})\neq0$

Für $f''(x_{E})$ < 0 ⇒ Hochpunkt

Für $f''(x_{E})$ > 0 ⇒ Tiefpunkt

$f''(x)=-6x^2+5$

$f''(0)=-6\cdot0^2+5=5$
Da 5 > 0, existiert an dieser Stelle ein Tiefpunkt.

$f''\left( -\sqrt { \frac { 5 }{ 2 } } \right) = -6 \cdot { \left( -\sqrt { \frac { 5 }{ 2 } } \right) }^{ 2 }+5= -6 \cdot \frac { 5 }{ 2 } +5=-10$
Da -10 < 0, existiert an dieser Stelle ein Hochpunkt.

$f''\left(\sqrt { \frac { 5 }{ 2 } } \right) = -6 \cdot { \left(\sqrt { \frac { 5 }{ 2 } } \right) }^{ 2 }+5= -6 \cdot \frac { 5 }{ 2 } +5=-10$
Und auch hier existiert ein Hochpunkt. Das verwundert nicht, weil der Graph der Funktion achsensymmetrisch zur y-Achse ist → Symmetrie.

ACHTUNG! Bei manchen Funktionen geht die schnelle Methode mit der zweiten Ableitung nicht. Dann hilft nur die Untersuchung der ersten Ableitung auf Vorzeichenwechsel links- und rechtsseitig der möglichen Extremstellen, z.B:

$f'(1)=-2\cdot1^3+5\cdot 1=3$

$f'(2)=-2\cdot2^3+5\cdot 2=-16+10=-6$

Bei einem Vorzeichenwechsel $\oplus \longrightarrow \circleddash$ hat die Funktion einen Hochpunkt. Umgekehrt einen Tiefpunkt.

Da ein Punkt immer aus einer Stelle und dem Funktionswert an dieser Stelle besteht, bedarf es noch der Berechnung der Funktionswerte. Man setzt dazu die gefundenen Extremstellen in die Ausgangsfunktion ein:

$f(0)=3$ damit erhalten wir die Koordinaten des einzigen Tiefpunkts: $T(0|3)$

$f\left( -\sqrt { \frac { 5 }{ 2 } } \right)=6{,}125$ des ersten Hochpunkts $H_{1}(-1{,}58|\, 6{,}125)$

$f\left( \sqrt { \frac { 5 }{ 2 } } \right)=6{,}125$ und die, des zweiten Hochpunkts $H_{2}(1{,}58|\, 6{,}125)$

Schließlich sei hier noch auf verschiedene Begriffe verwiesen, deren Bedeutungen nicht immer klar sind, da sie in Mathebüchern vermischt auftreten:

Stelle x	Funktionswert f(x)	Punkt E(x\|f(x))
Extremstellen:	Extrema:	Extrempunkte:
– Minimalstelle	– Minimum	– Tiefpunkt
– Maximalstelle	– Maximum	– Hochpunkt

Fortsetzung folgt!