Das Tangentenproblem

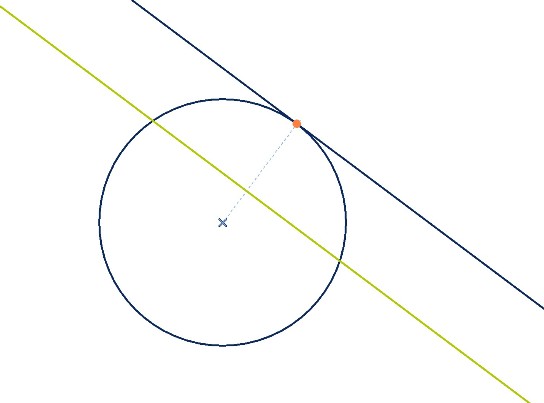
Im Rahmen einer Funktionsanalyse bzw. Kurvendiskussion kommen zwei Arten von Geraden, die man in Verbindung mit dem Kreis kennengelernt hat, wieder ins Spiel: Die Sekante und die Tangente. Die Sekante schneidet die Kreislinie an zwei Punkten, die Tangente berührt die Kreislinie an genau einem Punkt:

Im Gegensatz zu Geraden – Graphen von linearen Funktionen – haben Kurven an verschiedenen Punkten nicht dieselbe Steigung. Man stelle sich dazu den Querschnitt einer Skaterbahn vor:

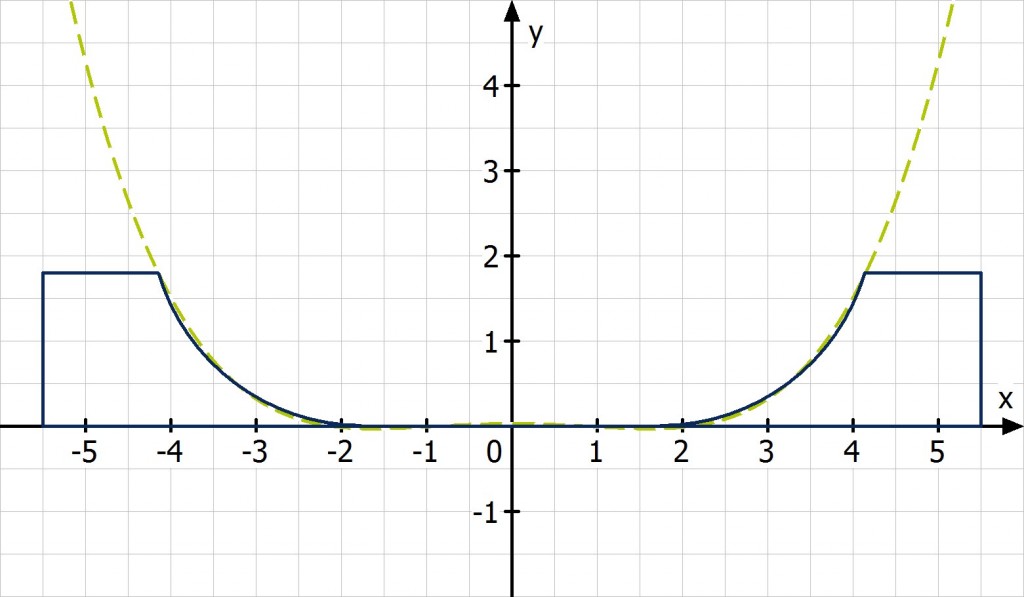
Zu Beginn der Fahrt geht es steil bergab, dann wird die Kurve immer flacher. Auf der anderen Seite dreht sich das Ganze um, dort steigt sie immer mehr an. Der Mathematiker bezeichnet diesen Verlauf als monoton fallend bzw. monoton steigend.

Je steiler die Bahn, desto betragsmäßig größer ist die Steigung, mal negativ (bergab), mal positiv (bergauf). Am tiefsten Punkt, am Boden, ist die Steigung null.

Möchte man nun gerne die Steigung an einem bestimmten Punkt wissen, braucht man als Hilfsmittel die Tangente. Da diese eine Kurve nur an einem Punkt berührt, ist die Steigung der Tangente identisch mit der Steigung an diesem Punkt:

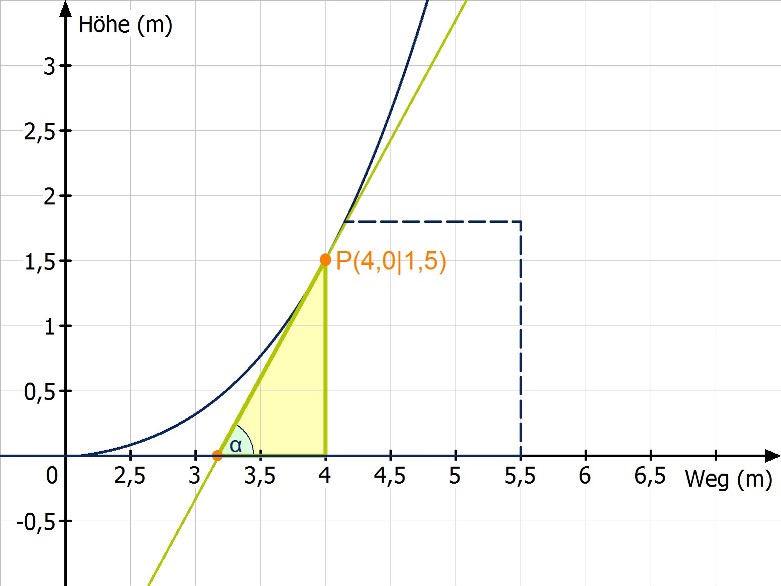
Steigung wird in der Regel mit „m“ bezeichnet. Das m taucht auch in der allgemeinen Geradengleichung auf:

y=mx+b

Die Frage, die sich allerdings stellt, ist: Woher weiß ich, wie groß die Steigung der Tangente ist, wenn ich nur einen Punkt kenne? Der zweite Punkt – der im obigen Schaubild auf der x-Achse liegt – ist frei gewählt. Würde man ihn nur etwas nach links oder rechts verschieben, wäre die Gerade keine Tangente mehr, sondern eine Sekante:

grün: Tangente, hellblau: Sekante

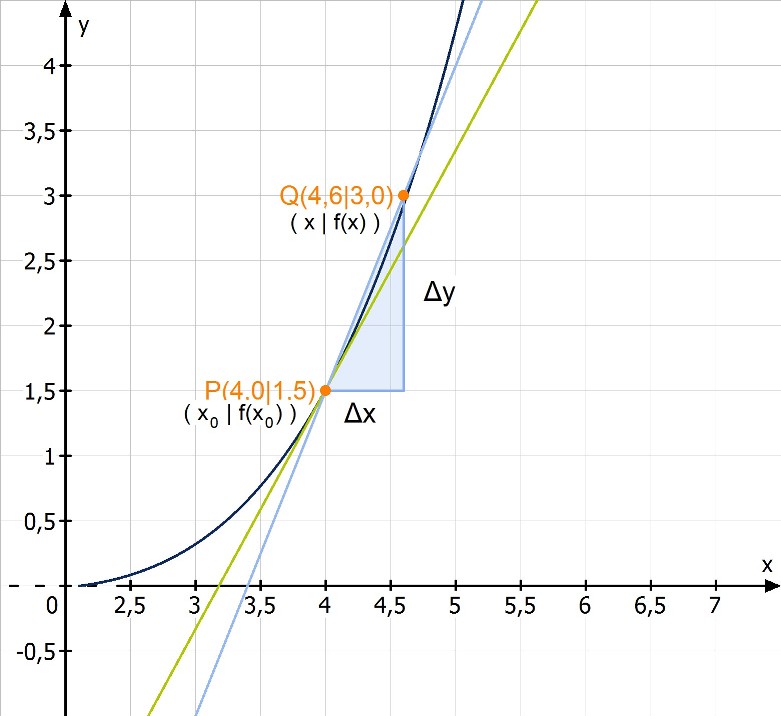
Man löst dieses Problem, indem man Punkte der Kurve wählt, die dem gesuchten Punkt immer näher kommen. Dabei verringert sich sowohl der horizontale, als auch der vertikale Abstand dieser zwei Punkte zueinander:

Der Quotient aus dem Höhenunterschied (Abstand der y-Werte) und dem Horizontalunterschied (Abstand der x-Werte) zweier Punkte bezeichnet man als Differenzenquotient. Er gibt die mittlere bzw. durchschnittliche Steigung (Änderungsrate) an: 

m_s=\tan \alpha=\dfrac{\Delta y}{\Delta x}=\dfrac{y-y_0}{x-x_0}=\dfrac{f(x)-f(x_0)}{x-x_0}

Das \Delta Zeichen steht für Differenz, sprich: "Delta"

Wie schon gesagt, wir brauchen zwei Punkte! Wären sie beide identisch, dann wäre sowohl die Differenz des Zählers, als auch die des Nenners null. Man könnte aber nicht weiter rechnen, weil man durch 0 nicht teilen kann (nicht definiert).

Suchen wir uns also z.B. einen Punkt in unmittelbarer Nähe des gesuchten Punktes
aus, dann können wir die Steigung der Sekante als eine gute Näherung zur Tangentensteigung berechnen:

m_s=\dfrac{\Delta y}{\Delta x}= \dfrac{f(x_0+ \Delta x)-f(x_0)}{\Delta x}

In unserem Beispiel ist: 

m_1=\dfrac{\Delta y}{\Delta x}= \dfrac{f(4,0+0,6)-f(4,0)}{0,6}=\dfrac{3,0-1,5}{0,6}=2,5

Würden wir uns einen noch näheren Punkt zu P aussuchen, mit \Delta x = 0,1, dann bekämen wir einen noch besseren Näherungswert für die Steigung im Punkt P:

m_2=\dfrac{\Delta y}{\Delta x}= \dfrac{f(4,0+0,1)-f(4,0)}{0,1}=\dfrac{1,7-1,5}{0,1}=2

Wenn wir also \Delta x immer kleiner wählen \Delta x \to 0, dann können wir die Steigung der Tangente und damit die Steigung an dem bestimmten Punkt berechnen, weil damit die Tangentensteigung m_t der Grenzwert der Sekantensteigung m_s ist. Man nennt diesen Grenzwert Differenzialquotient oder auch momentane Änderungsrate:

m_t=\displaystyle\lim_{\Delta x \to 0}\dfrac{\Delta y}{\Delta x}=\displaystyle\lim_{\Delta x \to 0}\dfrac{f(x_0+ \Delta x)-f(x_0)}{\Delta x}

Sprich: Limes von ... für Delta x gegen 0

Man bezeichnet diesen Grenzwert als Ableitung der Funktion an dieser Stelle: f'(x_0)

Einfacher geht es mit der alternativen Schreibweise \Delta x =h, der sogenannten
h-Methode: 

f'(x_0)=\displaystyle\lim_{h \to 0}\dfrac{f(x_0+h)-f(x_0)}{h}

Für eine Annäherung von links sähe der Differenzialquotient mit der h-Methode so aus: 

f'(x_0)=\displaystyle\lim_{h \to 0}\dfrac{f(x_0)-f(x_0-h)}{h}

Wenn man mit der Ableitung die Steigung der Tangente berechnen kann, dann gilt:

f'(x_0)=m_t

Oft wird nach der Gleichung der Tangente gefragt. Das m berechnet man mit Hilfe der Ableitungsfunktion, den Schnittpunkt mit der y-Achse durch Einsetzen der Punkt-Koordinaten, danach formt man nach b um:

t(x)=y=m_tx+b

Schneller geht es mit der Tangenten-„Zauberformel“:

t(x)=f'(x_0)\cdot(x-x_0)+f(x_0)

x_0 ist die Stelle des Berührpunktes

 

Nach oben