Zusammenhang Ableitungen
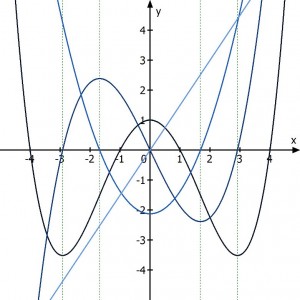
Wenn man sich ins Gedächtnis ruft, worum es bei der Ableitung geht – um Steigung einer imaginären Tangente und damit um die Steigung an einem bestimmten Punkt der Kurve – dann kann man sich damit gute Eselsbrücken bauen. Die Abbildung zeigt die Ausgangsfunktion mit ihrer ersten, zweiten und dritten Ableitung:
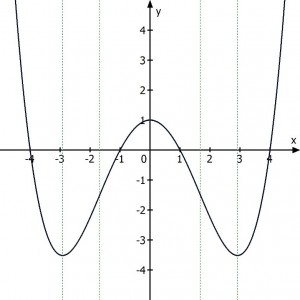 |
ExtremstellenDer Graph der ersten Ableitung der Funktion schneidet genau dort die x-Achse, wo der Graph der Funktion lokale Extremstellen besitzt, weil an diesen Stellen die Steigung null ist (notwendige Bedingung). Sind zudem die Funktionswerte der zweiten Ableitung an diesen Stellen positiv, hat der Graph der Funktion einen oder mehrere Tiefpunkt(e). Sind sie negativ, hat er einen oder mehrere Hochpunkt(e). MonotonieDort, wo die Funktionswerte der ersten Ableitung positiv sind, ist der Graph der Funktion streng monoton steigend. Im Intervall negativer Funktionswerte, ist der Graph der Funktion streng monoton fallend. WendestellenDer Graph der zweiten Ableitung der Funktion schneidet genau dort die x-Achse, wo der Graph der Funktion seine Wendepunkte besitzt (notwendige Bedingung). Sind zudem die Funktionswerte der dritten Ableitung ungleich null, hat der Graph der Funktion einen oder mehrere Wendepunkt(e). KrümmungDort, wo die Funktionswerte der zweiten Ableitung positiv sind, ist der Graph der Funktion eine Linkskurve. Im Intervall negativer Funktionswerte, ist der Graph eine Rechtskurve. |
 |
|
 |
|
 |
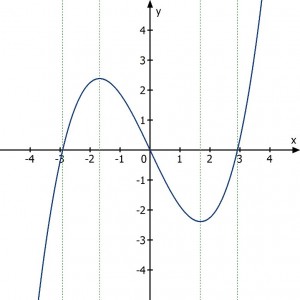
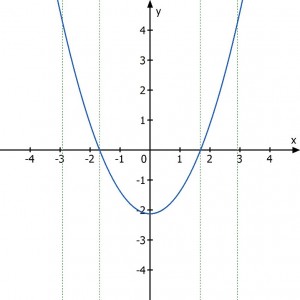
Man erkennt, dass der Grad der Funktion mit jeder weiteren Ableitung um eins abnimmt: