Typen reeller Funktionen

Wenn man eine Funktion graphisch darstellt, erkennt man bereits an der Form, wie sich der Verlauf mit größer oder kleiner werdendem x verändert. Manche Graphen sind gerade, manche kurvig, achsen- oder punktsymmetrisch, nähern sich einer gedachten Gerade, ohne sie zu je berühren. Sie weisen mitunter Lücken auf oder machen Sprünge. Das Schaubild zeigt die Graphen der wichtigsten Funktionstypen:

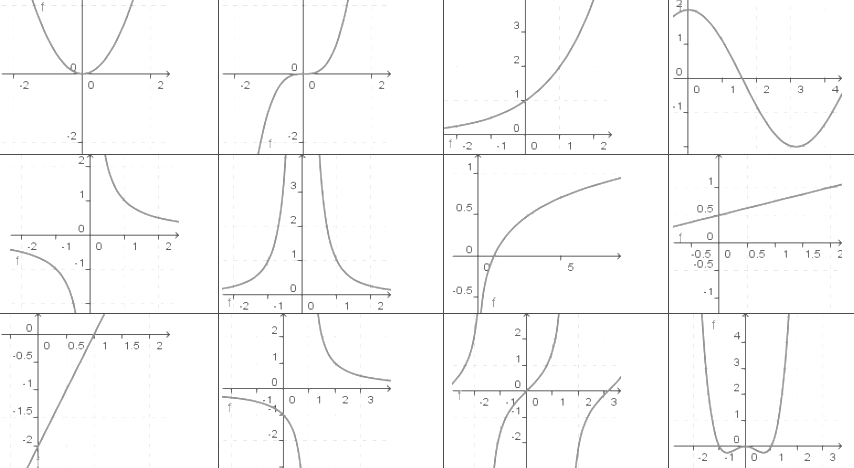
Funktionsgraphen — Quelle: http://www.roro-seiten.de

Die Funktionsterme lauten (von links nach rechts und oben nach unten): $x^2, x^3, 2^x, 2\,cos(x),\frac{1}{x}, \frac{1}{x^2}, lg(x), \frac{1}{4}x+\frac{1}{2}, 2x-2, \frac {1}{x-1}, tan(x), x^4-x^2$ .

Man fasst diese Typen reeller Funktionen nach Funktionsklassen zusammen. Die folgende Übersicht zeigt eine mögliche Einteilung:

Reelle Funktionen

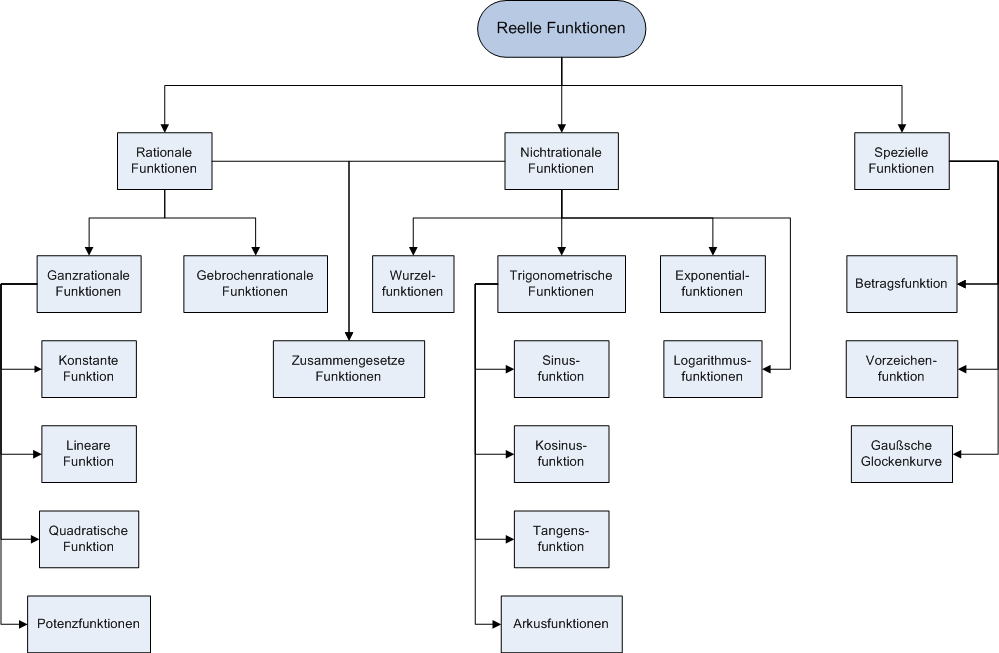
In der Oberstufe befasst man sich überwiegend mit rationalen Funktionen. Im Abitur werden meist Aufgaben mit Exponential- und Logarithmusfunktionen zu lösen sein.

Ganzrationale Funktionen

Bei ganzrationalen Funktionen – auch Polynomfunktionen genannt – sieht der Globalverlauf im Groben wie folgt aus. Man beachte, dass die Geraden oder Kurven je nach Funktion von den gezeigten abweichen und auch nicht zwingend – wie hier abgebildet – symmetrisch sind. Trotzdem macht es Sinn zu wissen, wie der Graph der Funktion vermeintlich aussehen wird, wenn man eine Kurvendiskussion zur Aufgabe hat.

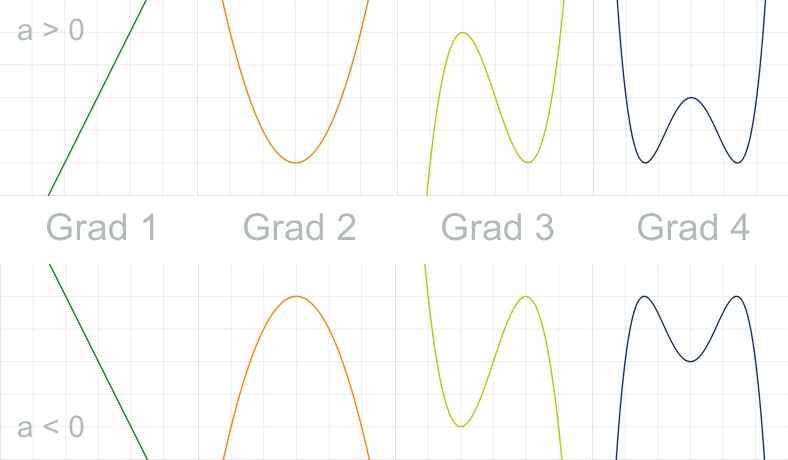
Aussehen ganzrationaler Funktionen

a ist der Koeffizient vor der Potenz mit der größten Hochzahl