Rotationsvolumen

Mit der Integralrechnung kann man die Fläche zwischen einem Graphen einer Funktion und der x-Achse berechnen. Lässt man diese Kurve um die x-Achse drehen (rotieren), entsteht ein sogenannter Rotationskörper, dessen Volumen sich mit folgender Formel berechnen lässt:

$V=\pi\int\limits_{a}^{b}\!(f(x))^2dx$

Fallbeispiel: Eine Glasmanufaktur bekommt den Auftrag, einen neuen Champagnerkelch zu entwerfen. Er soll 0,1 l Inhalt fassen und eine Trompetenform haben. Der Designer schlägt eine Kurvenform vor, die folgender Exponentialfunktion entspricht:

$f(x)=\frac{1}{2}e^{\frac{1}{8}x}=0,5e^{0,125x}$

Aus Vereinfachungsgründen betrachtet man dabei nur die Innenwand. Die x-Achse gibt die Höhe des Körpers bzw. den Füllstand an. Wie hoch muss der Kelch mindestens sein (gerundet auf ganze cm) damit oberhalb des Füllstriches noch 2 cm Platz sind?

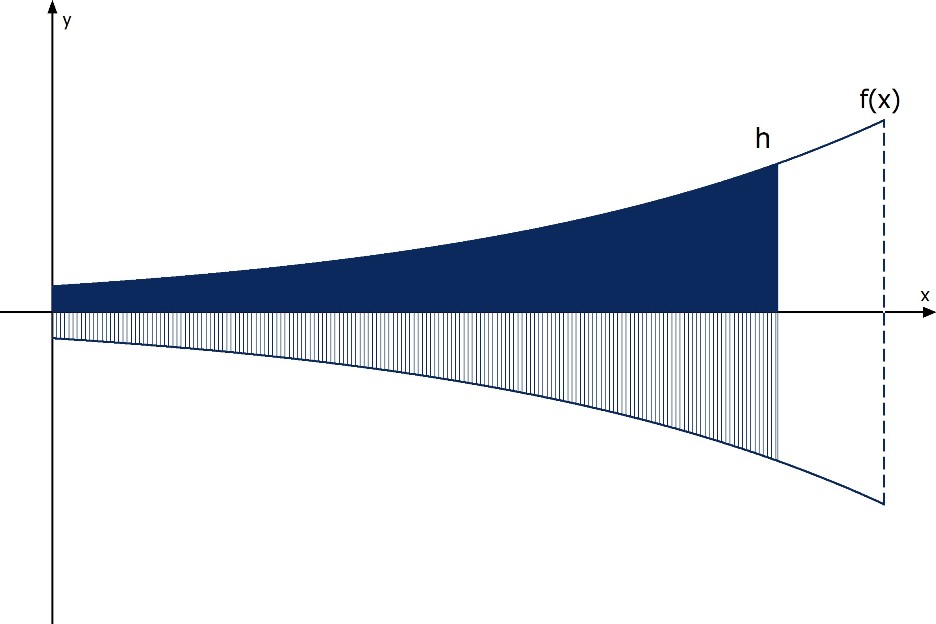
Integral: Rotationsvolumen

Da die Höhe gesucht und das Volumen gegeben ist, muss der Ansatz wie folgt lauten:

$V=\pi\int\limits_{0}^{h}(\frac{1}{2}e^{\frac{1}{8}x)^2}dx=100$

Tipp:  0,1 l = 0,1 dm³ = 100 cm³

$V=\pi\int\limits_{0}^{h}(\frac{1}{4}e^{\frac{1}{4}x})dx=\pi\left [ e^{\frac{1}{4}x} \right ] _{0}^{h}=\pi\left(e^{\frac{1}{4}h}-e^0\right)=100$

Nun hat man nur noch folgende Gleichung nach h aufzulösen:

$\pi\left(e^{\frac{1}{4}h}-1\right)=100$
$e^{\frac{1}{4}h}-1=\frac{100}{\pi}$
$e^{\frac{1}{4}h}=1+\frac{100}{\pi}$
$\frac{1}{4}h\cdot ln(e)=ln\left(1+\frac{100}{\pi}\right)$
$\frac{h}{4}=ln\left(1+\frac{100}{\pi}\right)$
$h=4\cdot \left ( ln\left(1+\frac{100}{\pi}\right)\right)=13,965\approx 14$

Tipp:  ln(e)= 1

Der Kelch müsste folglich mindestens eine Höhe von 16 cm haben.