Steckbriefaufgaben
Mit einem Steckbrief sucht man nach einer Person, bei Steckbriefaufgaben in der Mathematik sucht man nach einer Funktion – genauer gesagt nach einer Funktionsvorschrift bzw. Funktionsgleichung. In diesem Artikel geht es um die Bestimmung von ganzrationalen Funktionen mithilfe gegebener Eigenschaften. Das ist eigentlich nichts anderes als die Umkehrung einer Kurvendiskussion.
Vorgehensweise:
1. Aufstellen der allgemeinen Funktionsgleichung
2. Ableitungen der allgemeinen Funktionsgleichung berechnen (nicht immer nötig)
3. Übersetzen der Bedingungen in Gleichungen
4. Gleichungssystem lösen
5. Ergebnisse in Funktionsgleichung einsetzen
1. Aufstellen der allgemeinen Funktionsgleichung
Zur eindeutigen Bestimmung einer ganzrationalen Funktion n-ten Grades benötigt man ebenso viele Gleichungen, wie man Koeffizienten zu bestimmen hat. Die Anzahl der Koeffizienten ergibt sich aus der allgemeinen Form.
Eine ganzrationale Funktion 4. Grades hat z.B. die allgemeine Form:
(5 Koeffizienten, also braucht man 5 Gleichungen)
Bei einer Funktion 3. Grades lautet sie demnach:
(Es werden nur 4 Gleichungen benötigt)
Soll der Graph der Funktion achsensymmetrisch zur y-Achse verlaufen, reduziert sich die Funktionsgleichung auf Potenzen mit geraden Exponenten:
Verläuft der Graph zudem durch den Ursprung, kann auch das freie Glied c weggelassen werden, da c = 0.
Bei einer zum Ursprung punktsymmetrischen Funktion enthält der Funktionsterm nur ungerade Exponenten ohne Absolutglied (der Koeffizient ohne x) und kann je nach Grad so aussehen: oder auch:
.
2. Ableitungen der allgemeinen Funktionsgleichung berechnen
Um die Ableitungsfunktionen bilden zu können, benötigt man das Wissen über die Potenzregel, die Faktorregel, die Konstantenregel und die Summenregel. Für eine Funktion 4. Grades sehen die ersten beiden Ableitungen wie folgt aus:
3. Übersetzen der Bedingungen in Gleichungen
Das Verfahren der Gleichungsermittlung kann man aus folgender Tabelle entnehmen. Die Vorgaben beziehen dabei auf eine Funktion 3. Grades ohne erkennbare Symmetrie. Man entnimmt die Vorgaben entweder direkt aus der Aufgabenstellung oder erschließt sie sich aus einer gegebenen Grafik.
| Vorgabe → | Bedingung → | Gleichung |
| Der Graph der Funktion schneidet die y-Achse bei Sy. Wenn man den Koeffizienten des freien Gliedes (hier d) bereits kennt, kann man ihn in den folgenden Gleichungen auch gleich durch die entsprechende Zahl ersetzen. Damit reduziert sich die Anzahl der benötigten Gleichungen. | ||
| |
||
| Der Graph der Funktion verläuft durch den Punkt P: | ||
| Der Graph der Funktion schneidet oder berührt die x-Achse an der Stelle xa ⇒ Nullstelle: | ||
| |
||
| Der Graph der Funktion berührt die x-Achse an der Stelle xe ⇒ Extremstelle ⇒ waagerechte Tangente ⇒ erste Ableitung gleich null: | ||
| |
|
|
| Hoch- oder Tiefpunkt mit gegebenen Koordinaten: | ||
| |
||
| Der Graph der Funktion hat an der Stelle xw die Steigung m: | ||
| Wendepunkt mit gegebenen Koordinaten: | ||
| |
||
| Ein Sattelpunkt ist ein besonderer Wendepunkt. An diesem Punkt ist sowohl die erste als auch die zweite Ableitung gleich null. | ||
| Eine Wendetangente ist die Tangente an einem Wendepunkt mit Steigung m. | ||
TIPP: In der Regel bekommt man nur so viele Vorgaben, wie man braucht. Wenn mehr Bedingungen erfüllt sein sollen, muss man auch alle in Gleichungen überführen. Fehlt dagegen eine Gleichung für eine eindeutige Lösung, führt man für das freie Glied einen Parameter z.B.: d = k ein.
4. Gleichungssystem lösen
Folgendes Gleichungssystem ist zu lösen. Hierzu sollte man sich noch einmal das Additionsverfahren (bei dem man auch subtrahieren darf) bzw. den Gauß’schen Algorithmus ansehen:
Da d = 0, reduziert sich das System auf drei Gleichungen mit drei Variablen:
| I. | | • 3 | ||
| II. | |||
| III. |
| I. – II. = I.* | |
| • 6 | |
| 3 x I. – III. = II.* |
| 6 x I.* – II.* | | : 12 | ||
| |
| a in I.* eingesetzt: | |
| + b, −4 | |
| a und b in I. eingesetzt: | |||
| | + 5 | |||
5. Ergebnisse in Funktionsgleichung einsetzen
Die Funktionsgleichung, die diese Bedingungen erfüllt, lautet demnach:
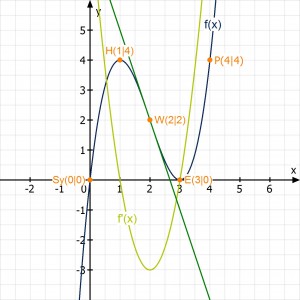
Die Grafik zeigt die Funktion (blau), die erste Ableitung (hellgrün), die Wendetangete (mittelgrün) und die verschiedenen Punkten mit ihren teilweise vorhandenen Doppeleigenschaften:
Es geht natürlich auch mithilfe eines Programms: Rechner für Steckbriefaufgaben von Arndt Brünner.
