Anwendungsaufgaben Funktionen
Schüler bekommen meist dann Probleme, wenn es darum geht, das Erlernte auf eine reale Situation anzuwenden. Sie lernen, welche Funktionen es gibt, haben aber keinen blassen Schimmer, wozu diese gut sind. Viele Oberstufenschüler können auf Anhieb alle Ableitungen berechnen – aber warum man das macht, wissen sie nicht. Es ist schon ein bisschen traurig, dass man ein Werkzeug in die Hand bekommt, mit dem man nicht umgehen kann.
Beispiel für lineare Funktionen:
Funktionen begegnet man bereits in der 8. Klasse. Eine lineare Funktion könnte z.B. angeben, wie viel Geld man mit dem Verkauf von x Stücken Kuchen bei einem Schulfest verdient. Kostet ein Stück 1,20 €, dann könnte man mit folgender Funktion den Umsatz bzw. Erlös des Kuchenverkaufs berechnen:
Was hochmathematisch aussieht, beschreibt mit einem Funktionsterm, wie man auch ohne Kenntnisse über Funktionen rechnen würde: die Anzahl der verkauften Kuchenstücke mit dem Stückpreis multiplizieren.
Wenn man den Zusammenhang zwischen Anzahl der verkauften Stücke und Umsatz – also den Funktionsterm – kennt, hat das den Vorteil, dass man damit den Umsatz für eine beliebige Anzahl sofort berechnen kann – weil der Umsatz von dieser Menge abhängig ist.
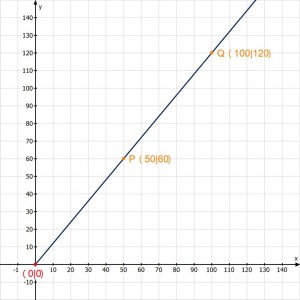
Der Graph der Funktion ist eine Gerade, die durch den Ursprung (0|0) geht:
Man kann an einem Graphen einer Funktion Folgendes sofort ablesen bzw. erkennen:
1. Schnittpunkt mit der y-Achse:
beschreibt die Ausgangssituation.
2. Schnittpunkt mit der x-Achse:
Die sogenannte „Nullstelle“ gibt an, wo etwas „am Boden“ bzw. gleich null ist.
3. Steigung: ist sie konstant? Steigt oder fällt der Graph von links nach rechts gesehen? Ist der Graph eine Gerade oder eine Kurve wie im nächsten Beispiel …
Beispiel für quadratische Funktionen:
Die Abbildung zeigt einen Querschnitt einer Bahnunterführung, die 5,50 m breit und 4,50 m hoch ist. Eine Fragestellung könnte sein: Passt ein 2,50 m breiter und 3,70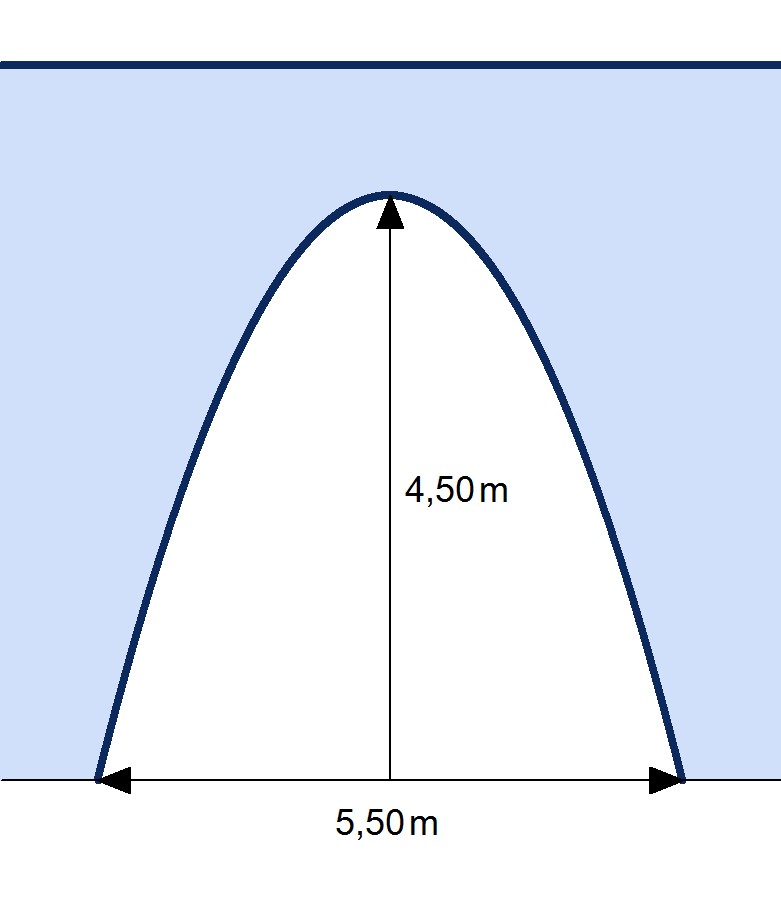 
m hoher LKW mittig hindurch?
Die Krümmung des Bogens entspricht einer nach unten geöffneten Parabel. Allerdings ist die Funktionsvorschrift noch unbekannt und muss daher zuerst bestimmt werden.
Legt man über dieses Bild ein Koordinatensystem, kann man den Funktionsterm anhand ausgewählter Punkte ermitteln. Sinnigerweise wählt man dazu die Lage der Achsen so, dass sie mit Boden und Höhe übereinstimmen.
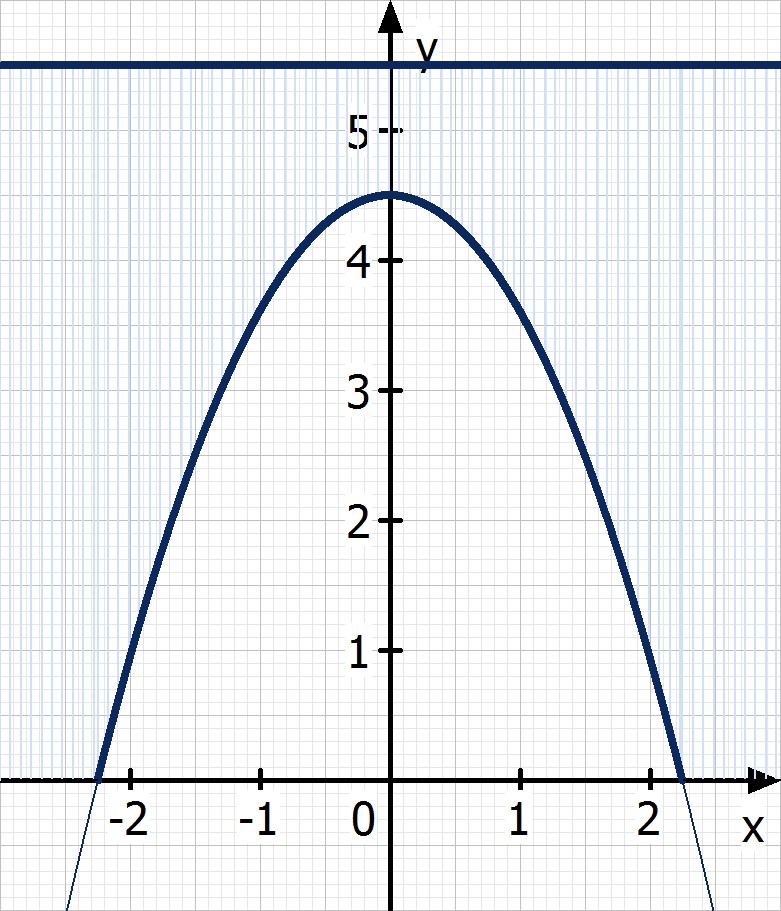
Wie kommt man nun auf die Funktionsvorschrift?
1. Schnittpunkt mit der y-Achse:
Der Graph schneidet die y-Achse im Punkt Sy (0|4,5). Das bedeutet, die Funktion hat an der Stelle x = 0 den Wert 4,5:
2. Schnittpunkte mit der x-Achse:
Wegen der Achsensymmetrie zur y-Achse haben die Nullstellen denselben Betrag.
Er ist halb so groß, wie die gesamte Breite der Unterführung:
Die allgemeine Form einer quadratischen Funktion, deren Graph symmetrisch zur y-Achse und gegenüber der Normalparabel getreckt oder gestaucht ist, lautet:
Eingesetzt, ergibt sich daraus: 
Da c bekannt ist, muss die zweite Gleichung nur noch nach a umgeformt werden:
