Die Wurfparabel

Maximale Höhe einer Wurfparabel berechnen

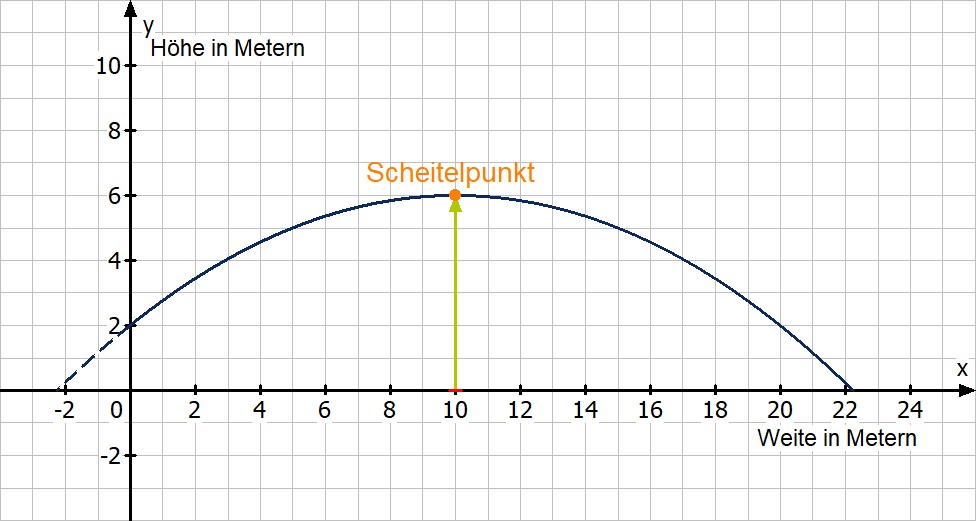
Scheitelpunkt einer Wurfparabel

Gegeben:	Quadratische Funktion in Polynomform: $f(x)=ax^2+bx+c$
Gesucht:	Maximale Höhe: Frage nach dem Scheitelpunkt einer nach unten geöffneten Parabel
Lösungsansatz 1:	Scheitelpunktform mit Hilfe der quadratischen Ergänzung bestimmen, Scheitelpunkt ablesen
Lösungsansatz 2:	Maximum mit Hilfe der Ableitung berechnen (folgt)

Ansatz mit Scheitelpunktform

Grundwissen:

Scheitelpunktform (SPF): $f(x)=a(x-d)^2+e$
Scheitelpunkt aus der Scheitelpunktform ablesen können: $S(d|e)$
Binomische Formeln (1. und 2.):
$(a+b)^2=a^2+2ab+b^2$ und $(a-b)^2=a^2-2ab+b^2$
Eventuell: Division eines Bruchs durch eine ganze Zahl
(in diesem Fall durch 2, dabei verdoppelt sich der Nenner)
Eventuell: Quadrieren eines Bruchs
(Zähler und Nenner mit sich selbst multiplizieren)
Ausklammern (Faktorisieren) und Klammern ausmultiplizieren: $a(b+c)=ab+ac$ und $a(b-c)=ab-ac$

Vorgehensweise Rechnung:

Den Faktor vor dem x² ausklammern
(wenn vor dem x² ein Faktor oder ein Minuszeichen steht)
Das b der binomischen Formel ermitteln
(Die Zahl, die in der Klammer vor dem x steht, durch 2 teilen)
Das Quadrat davon bilden, ergänzen und wieder abziehen
Binomische Formel anwenden und die zweite Potenz ausrechnen
Zusammenfassen
Äußere Klammer ausmultiplizieren
Scheitelpunkt aus SPF ablesen. Der y-Wert ist das gesuchte Ergebnis

Zahlenbeispiel:

$f(x)=-\frac{1}{25}x^2+\frac{4}{5}x+2$

Die größte Herausforderung dürfte bereits das Ausklammern darstellen. Das Rechnen mit Brüchen wird das Ganze noch erschweren. Folgende Fragen helfen den richtigen Term für die Klammer zu finden:

$-\frac { 1 }{ 25 } \cdot \boxed { \frac { }{ } } =-\frac { 1 }{ 25 }x^2\ ?$

$-\frac { 1 }{ 25 } \cdot \boxed { \frac { }{ } } =\frac { 4 }{ 5 } x\ ?$

$-\frac { 1 }{ 25 } \cdot \boxed { \frac { }{ } } =2\ ?$

Die Lösung dieser Fragen bringt die Umkehroperation, die Divison, Beispiel:

$\frac { 4 }{ 5 } x : (-\frac { 1 }{ 25 })=\frac { 4 }{ 5 } x\cdot(-\frac { 25 }{ 1})=\frac{4x\cdot(-25)}{5}=4x\cdot(-5)=-20x$

Noch schneller geht es, wenn man die Brüche in Dezimalzahlen umwandelt:

$0,8x : (-0,04)=-20x$

In der weiteren Rechnung soll hier aber mit Brüchen gerechnet werden, weil dies die von Lehrern bevorzugte Variante ist und eben auch zeigt, dass man die Bruchrechnung beherrscht.

Die Funktion kann folglich auch so geschrieben werden:

$f(x)=-\frac{1}{25}(x^2-20x-50)$

Für die quadratische Ergänzung interessiert zu Beginn bloß der normierte Term in der Klammer. Der Faktor davor wird vorerst nur mitgeführt.

Man ergänzt das Quadrat des halben Faktors von x damit daraus eine binomische Formel wird und zieht ihn gleich wieder ab, damit sich der Wert des Terms nicht ändert:

$f(x)=-\frac{1}{25}(x^2-20x+10^2-10^2-50)$

Zur Erinnerung:		$a^2-2ab+b^2$	=	$(a-b)^2$
$x^2-20x+10^2$	=	$x^2-20x+100$	=	$(x-10)^2$

$f(x)=-\frac{1}{25}\left[(x-10)^2-10^2-50\right]$ $f(x)=-\frac{1}{25}\left[(x-10)^2-100-50\right]$ $f(x)=-\frac{1}{25}\left[(x-10)^2-150\right]$

Jetzt noch die äußere, eckige Klammer ausmultiplizieren:

$f(x)=-\frac{1}{25}(x-10)^2+6$

Der Scheitelpunkt kann aus dieser Form direkt abgelesen werden. Er hat die Koordinaten $S (10| 6)$ . Da der Funktionswert an der Stelle x = 10 die maximale Höhe angibt, ist die Lösung: y = 6. Das Objekt steigt bis zu einer Höhe von 6 Metern über dem Boden an.

Aufgaben zum Üben:

Bei der Auswahl der Übungsaufgaben wurden verschiedene Schwierigkeitsgrade berücksichtigt, wie sie auch in Klassenarbeiten vorkommen:

$f(x)=-2x^2+8x-6$
$f(x)=6x-0,5x^2$
$f(x)=-x^2-10x-17$
$f(x)=-\frac{1}{2}x^2-x+4$

Ein Arbeitsblatt fürs schrittweise Vorgehen kann man sich hier downloaden.

Weitere Übungsaufgaben mit Lösungen findet man bei Brinkmann

Wer seine Lösungen überprüfen will: Online-Rechner

Kleines Übungstool findest du hier: LearningApps