Gauß-Algorithmus

Spätestens wenn man Gleichungssysteme (LGS) mit drei oder mehr Gleichungen lösen will, bekommt man mit den bisher bekannten Verfahren Probleme. Die Fortführung des klassischen Additionsverfahrens ist der Gauß–Algorithmus. Man nennt dieses Verfahren auch Gaußsches Eliminationsverfahren, denn es fallen schrittweise Variablen weg. Der Vorteil dieses Verfahren liegt u.a. darin, dass man sich das Notieren der Variablen sparen kann. Das Anlegen einer Tabelle bzw. Matrix reicht aus. Da eine lineare Gleichung nur dann eindeutig lösbar ist, wenn sie nur eine Unbekannte enthält, versucht man eine sogenannte Stufenform herzustellen. Folgende Operationen sind dabei erlaubt:

• Zeilen vertauschen. Das bringt Vorteile, wenn in Zeilen bereits Nullen vorkommen.
• Spalten vertauschen. Das sollte man – wenn überhaupt – nur zu Beginn machen und daran denken, die Spalten entsprechend umzubenennen.
• Äquivalenzumformung. Man kann jede Gleichung mit einer Zahl multiplizieren oder durch eine Zahl teilen – natürlich beide Seiten – sie bleibt wertgleich.
• Gleichungen können addiert oder voneinander subtrahiert werden, wichtig ist, dass man nur solche Gleichungen nimmt, bei denen bereits zwei Nullen übereinander stehen (Ausnahme: erste Addition).

Auch wenn man einiges darf, ist es nicht unbedingt sinnvoll – besonders als Anfänger – dies auch zu tun. Wer sichergehen will, hält sich am besten an die folgende oder eine ihr verwandte Vorgehensweise:

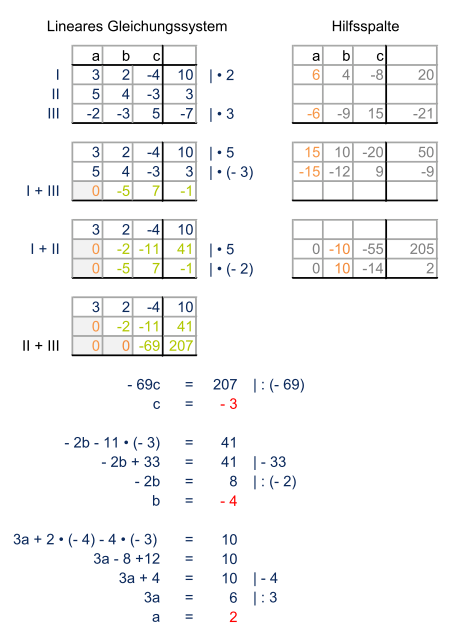
Die Ergebniszeilen sind grün dargestellt

Zuerst versucht man in einer Spalte eine Null zu erzeugen. Das klappt, indem man das kleinste gemeinsame Vielfache (kgV) der Zahlen der ersten und dritten (bzw. ersten und zweiten) Gleichung findet und beide Gleichungen entsprechend umformt. Möchte man gleich zwei Nullen auf einen Streich erzeugen, sucht man nach dem kgV aller Zahlen dieser Spalte. Wer lieber addiert als subtrahiert, sollte darauf achten, dass dann das kgV betragsmäßig gleich, aber das Vorzeichen unterschiedlich sein muss.

Die Hilfsspalte zeigt die jeweils umgeformten Gleichungen, die dann entweder addiert oder voneinander subtrahiert werden. Man schreibt diese normalerweise nicht auf, sondern rechnet die Operationen im Kopf.