Trigonometrische Funktionen zeichnen

Wer vor der Aufgabe steht, den Graphen einer Winkelfunktion zu zeichnen, kommt schnell mal ins Schwitzen, denn diese können sich hinsichtlich folgender Punkte unterscheiden:

Amplitude
Periode oder Frequenz (Kehrwert der Periode)
Verschiebung in x-Richtung (Phasenverschiebung)
Verschiebung in y-Richtung

Die elementare Sinusfunktion: Die Sinuskurve

Trigonometrische Funktionen sind periodisch, d.h. es treten in gleichen Abständen wiederkehrend dieselben Funktionswerte auf. Die Sinusfunktion hat die Periode 2π. Ihre Funktionswerte liegen im Bereich -1 bis 1:

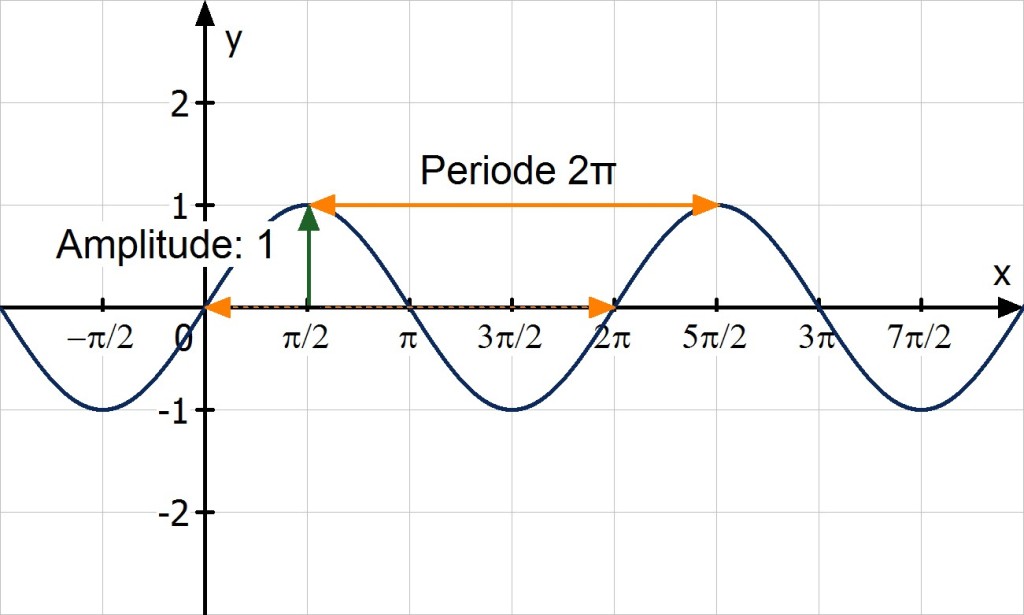
Sinuskurve 1

Man erkennt, dass dadurch auch die Extremstellen einen Abstand von 2π haben. Die Nullstellen liegen achsensymmetrisch dazu. Ihr Abstand beträgt 1π. Da die Sinuskurve durch den Ursprung geht, kann man die Lage der Nullstellen mit der Formel $x_k=k \cdot \pi$ sehr einfach berechnen.

Die allgemeine Sinusfunktion

U.a. in der Schwingungslehre begegnet man Sinusfunktionen der Form:

$f(x)=a\cdot sin(bx+c)+d$

Wobei die Kurvenparameter a, b, c und d verschiedene Veränderungen gegenüber der Sinuskurve bewirken:

a	b	c	d
Veränderung der Funktionswerte	Veränderung der Periodenlänge	Verschiebung in x-Richtung	Verschiebung in y-Richtung
$W=[-a;a]$	$p=\dfrac{2\pi}{b}$	$\pm \ \dfrac{c}{b}$	d > 0 ↑ d < 0 ↓

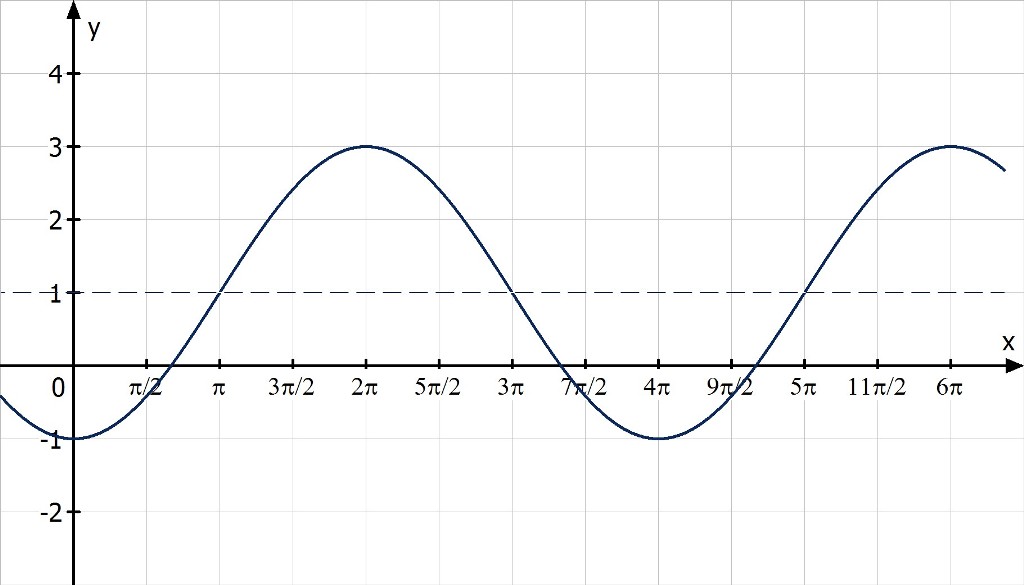
Beispiel: Folgende Funktion soll skizziert werden:

$f(x)=2\cdot sin(\frac{1}{2}x-\frac{\pi}{2})+1$

Eine Arbeitserleichterung bringt das Ausklammern, denn dann kann man die Phasenverschiebung direkt ablesen:

$f(x)=2\cdot sin\left(\frac{1}{2}(x-\pi)\right)+1$

Vorgehensweise

Es empfielt sich, die verschiedenen Veränderungen schrittweise einzuzeichnen.

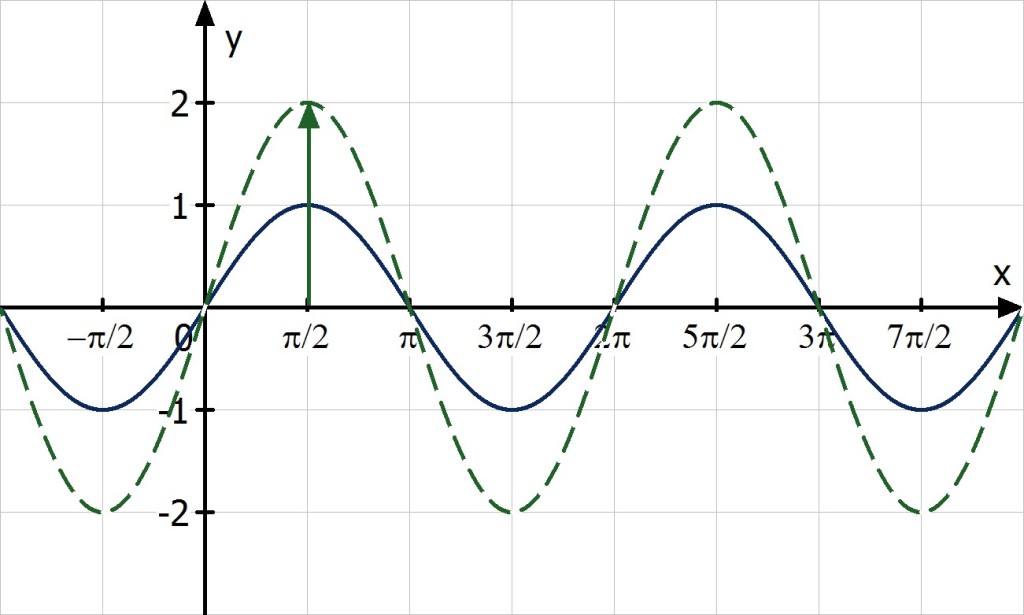
1. Veränderung der Funktionswerte (Amplitude)

Normalerweise ist die Amplitude 1, hier ist a = 2:

Hinweis : Für a < 0 ist der Graph der Funktion an der x-Achse gespiegelt.

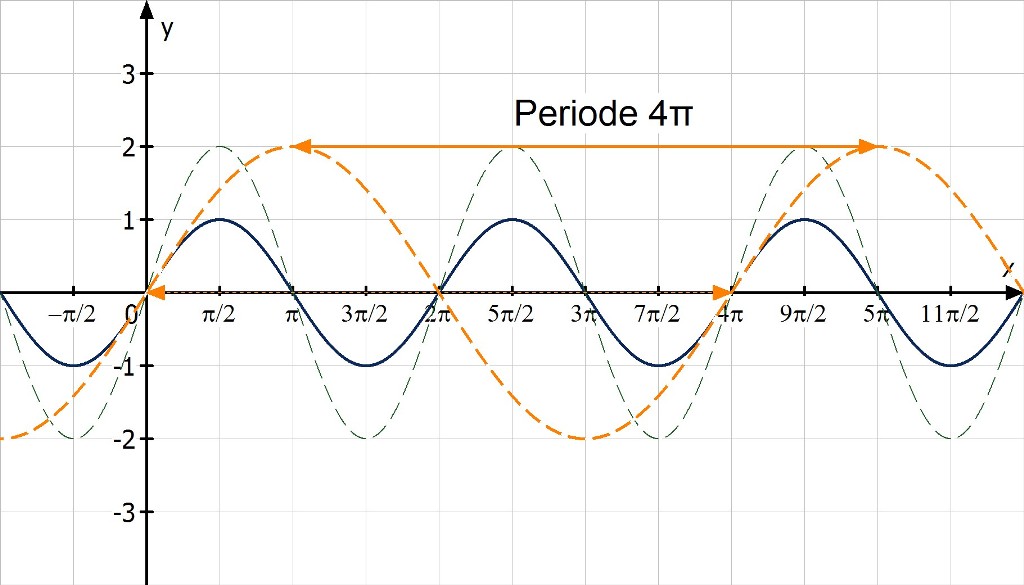
2. Veränderung der Periode

Diese Sinusfunktion ist gegenüber der elementaren Sinusfunktion in x-Richtung gedehnt. Die Periodenlänge beträgt:

$p=\dfrac{2\pi}{\frac{1}{2}}=2\pi\cdot\frac{2}{1}=4\pi$

Dadurch verändert sich auch die Lage der Nullstellen. Der neue Graph schneidet die x-Achse bei $x_k=k\cdot 2\pi$ . Diese zeichnet man am besten zuerst ein. Im Intervall $x_0+p$ liegt dann eine volle Schwingung:

Sinuskurve 3

3. Verschiebung in x-Richtung

Durch das Ausklammern von b kann man die Phasenverschiebung direkt ablesen. Der Graph der Funktion ist um 1π nach rechts verschoben. Das bedeutet, dass sowohl Nullstellen als auch Extremstellen um 1π nach rechts zu versetzen sind:

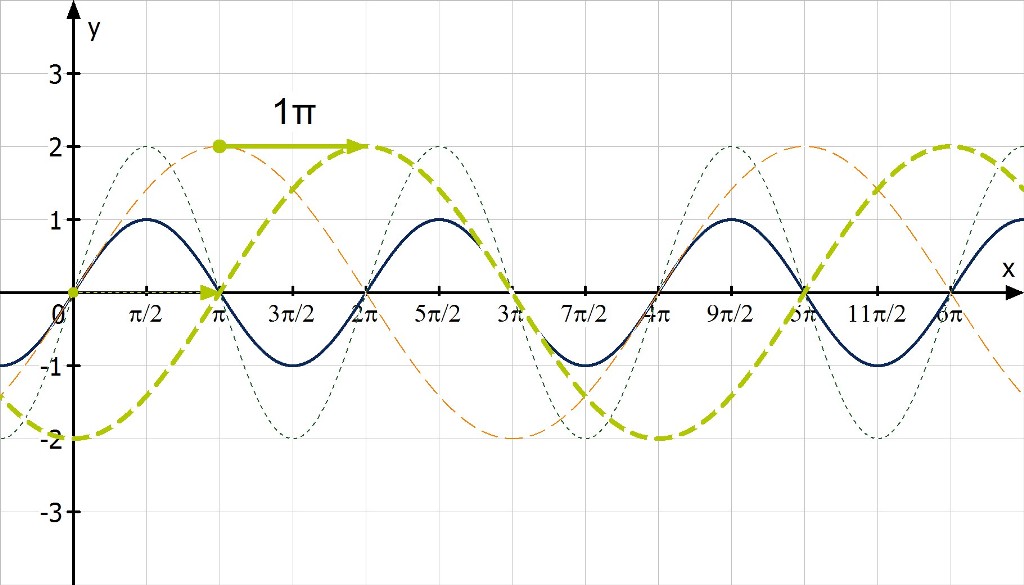
Sinuskurve 4

4. Verschiebung in y-Richtung

Für d > 0 verschiebt sich die gesamte Kurve um d Einheiten nach oben. Die Mittellinie liegt bei d = 1:

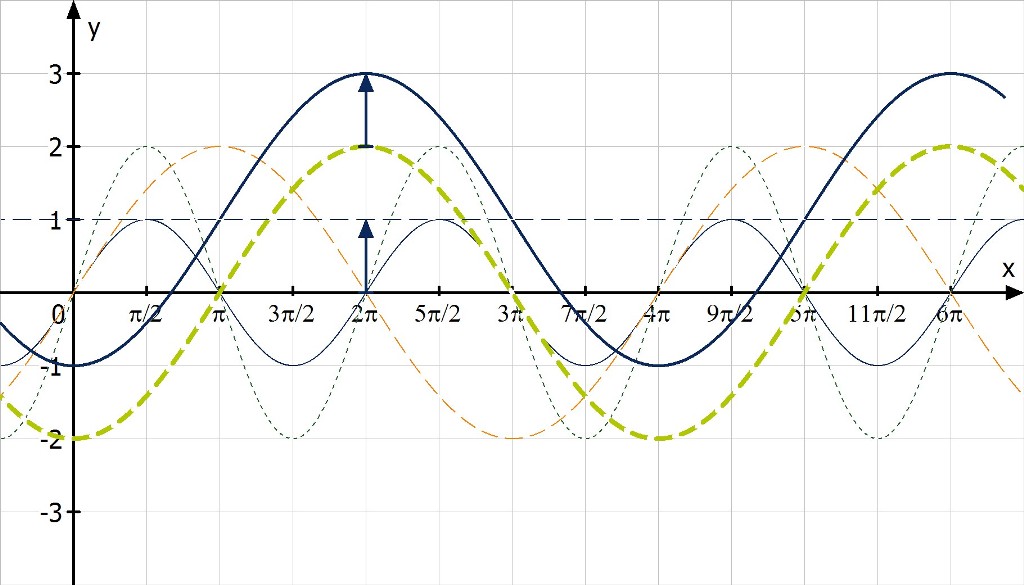
Sinuskurve 5

Damit ist das Aussehen der Funktion gefunden.

$f(x)=2\cdot sin(\frac{1}{2}x-\frac{\pi}{2})+1$

Sinuskurve 6