Praxisbeispiel: Klobrille

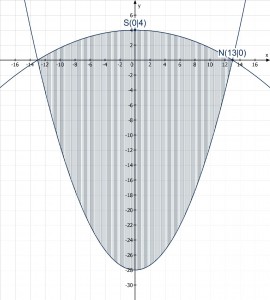
Eine etwas skurrile Fragestellung befasst sich mit dem Flächeninhalt einer Klosettöffnung. Die Abbildung zeigt die durch Messen ermittelte Form: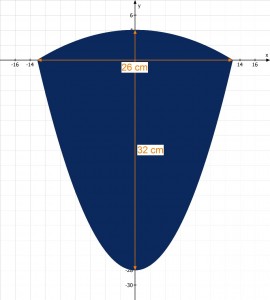

Eine grobe Schätzung durch Multiplikation der Abstände an der längsten und breitesten Stelle ließe einen Flächeninhalt von: $A_s=32cm\cdot26cm=832cm^2$ vermuten, aber das wäre nur eine schlechte Annäherung, denn es handelt sich hierbei um zwei aneinandergesetzte Parabeln, von denen eine nach oben, und eine nach unten geöffnet ist:

Was man zur weiteren Flächenberechnung braucht, sind die beiden Funktionsgleichungen der Parabeln und die Stammfunktion der Differenzfunktion. Den Flächeninhalt berechnet man dann mithilfe des Integrals.

Es muss sich bei beiden Kurven um Graphen quadratischer Funktionen handeln. Da diese gegenüber der Normalparabel lediglich vertikal verschoben, gestaucht und anders geöffnet sind, gilt folgender Zusammenhang:

$f(x)=ax^2+c$

Die Schnittpunkte der Graphen mit der y-Achse kann man aus der Zeichnung bzw. direkt aus den Koordinaten der Punkte ablesen, denn für jeden Punkt auf der Ordinate gilt: $x=0$

$f(0)=4\Rightarrow c=4$
$g(0)=-28\Rightarrow c=-28$

Mithilfe einer Nullstelle kann man dann auch den Parameter a berechnen, denn es gilt für solche Stellen immer: $f(x)=y=0$

$f(13)=0\Rightarrow 169a+4=0\Rightarrow a=-\frac{4}{169}$
$g(13)=0\Rightarrow 169a-28=0\Rightarrow a=\frac{28}{169}$

Die beiden Funktionsgleichungen sind damit gefunden:

Die obere lautet: $f(x)=-\frac{4}{169}x^2+4$
Die untere Lautet: $g(x)=\frac{28}{169}x^2-28$

Gesucht ist nun das Integral der Differenz beider Funktionen (obere minus untere Funktion) im Intervall −13 bis 13:

$A=\int\limits_{-13}^{13}(f(x)-g(x))dx$
TIPP: Wegen der Achsensymmetrie zur y-Achse kann man sich auf den positiven Bereich beschränken, wenn man das Ergebnis verdoppelt. Das verhindert lange, unüberschaubare Terme mit Minusklammer:

$A=2\cdot\int\limits_{0}^{13}(f(x)-g(x))dx$

Um das Integral berechnen zu können, braucht man die Stammfunktion der Differenzfunktion. Alternativ könnte man auch jedes Integral für sich berechnen und die orientierten Flächeninhalte addieren.

$d(x)=\left(-\frac{4}{169}x^2+4\right)-\left(\frac{28}{169}x^2-28\right)=-\frac{32}{169}x^2+32$

Die zugehörige Stammfunktion lautet:

$D(x)=-\frac{32}{169}\cdot\frac{1}{3}x^3+32x=-\frac{32}{507}x^3+32x$

Die Integrationskonstante c kann weggelassen werden

Das Integral (und damit der Flächeninhalt) berechnet sich nach dem Hauptsatz der Differenzial- und Integralrechnung:

$A=2\cdot\int\limits_{0}^{13}(-\frac{32}{169}x^2+32)dx=2\cdot\left [-\frac{32}{507}x^3+32x \right ] _{0}^{13}$
$=2\cdot\left[(-\frac{416}{3}+416)-0\right]=2\cdot\frac{832}{3}=554,\bar 6\ FE$

Die Öffnung ist also 555 cm² bzw. 0,0555 m² groß. Das entspricht in etwa der Größe der Öffnung eines gewöhnlichen, runden Putzeimers.