Die Umkehrfunktion

Bei einer Funktion wird jeder reellen Zahl x aus der Definitionsmenge genau eine reelle Zahl y aus der Wertemenge zugeordnet. Eine Funktion kann also an einer Stelle nicht verschiedene Funktionswerte haben! Bei der Umkehrfunktion sind die Rollen von x und y im Vergleich zur Ausgangsfunktion vertauscht. Daraus leitet sich ab, dass eine Funktion nur dann umkehrbar ist, falls es zu jedem

$y \in W_f$ nur ein $x \in D_f$ mit $f(x)=y$ gibt.

Den Graphen der Umkehrfunktion erhält man durch Achsenspiegelung an der Winkelhalbierenden: y = x. Auch die Koordinaten der Punkte einer Umkehrfunktion sind gegenüber der Ausgangsfunktion vertauscht – das hilft beim Zeichnen. Außerdem gilt:

$D_{\bar{f}}= W_f$ und $W_{\bar{f}}=D_f$

mit  Umkehrfunktion, man schreibt auch

Soll man eine Umkehrfunktion bestimmen, bedarf es folgender Schritte:

Untersuchung der Ausgangsfunktion auf Umkehrbarkeit (gibt es an verschiedenen Stellen denselben Funktionswert?).
Eventuell Definitionsbereich neu festlegen.
Definitonsbereich der Umkehrfunktion bestimmen (ist gleich des Wertebereichs der Ausgangsfunktion).
Gleichung: y = f(x) nach x auflösen.
Variablen tauschen.

Beispiel: $f(x)= (x+2)^2$

Es handelt sich dabei um eine nach links verschobene Normalparabel. Diese hat bekanntlich immer (bis auf x = -2) an zwei Stellen denselben Funktionswert. Man muss daher den Definitionsbereich auf einen „Arm“ einschränken:

$D_f=[-2\, ; \infty[$ $W_f=[\,0\, ; \infty [$

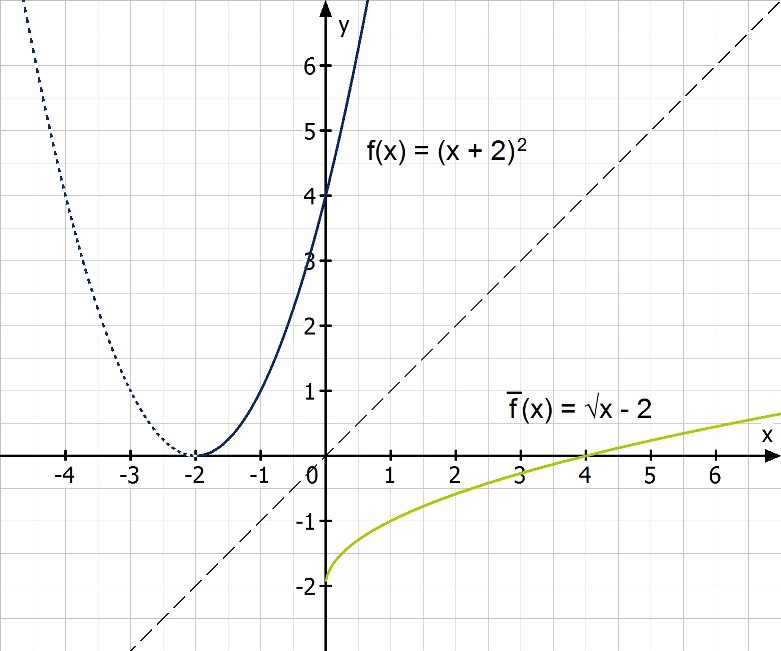
Da der Defnitionsbereich der Umkehrfunktion dem Wertebereich der Ausgangsfunktion entspricht, sind wir mit dem dritten Schritt schnell fertig:

$D_{\bar{f}}= [\,0\, ; \infty [$ $W_{\bar{f}}=[-2\, ; \infty[$

Nun wird die Gleichung umgeformt:

$y = (x+2)^2$

$\sqrt{y}=x+2$

$\sqrt{y}-2=x$

Zum Schluss noch die Variablen vertauschen, und schon hat man die Umkehrfunktion bestimmt:

$y={\bar{f}}(x)=\sqrt{x}-2$

Für Fortgeschrittene: Wer sich bereits mit Ableitung und Monotonieverhalten auskennt, kann sich bei der Bestimmung der Umkehrbarkeit auch diesen Satz zunutze machen: Jede streng monotone Funktion ist umkehrbar.

Streng monoton steigend ist eine Funktion in einem bestimmten Intervall, wenn gilt:
f'(x) > 0 , streng monoton fallend, wenn: f'(x) < 0.

Schreibt man die Funktion als Polynom auf:

$f(x)= x^2+4x+4$ und bildet die erste Ableitung, $f'(x)=2x+4$

dann braucht man lediglich zwei Ungleichungen lösen: Für welches x ist 2x + 4 > 0
bzw 2x + 4 < 0. Man muss sich dann nur noch für einen Bereich entscheiden, den steigenden oder fallenden.